Published: Thursday, 12 November 2020 11:27 | Print

SFT Statistical Field Theory

Low-Dimensional Systems, Integrable Models and Applications

Abstract

This project is centered on a series of outstanding questions of statistical field theory. Guiding lines are the exact non-perturbative methods of quantum field theory, based on the developments in conformal theories, exactly solvable lattice models and quantum integrable systems. A key feature of all these approaches is their ability to enlighten and account for strong coupling phenomena in quantum systems with infinite degrees of freedom. Applications of quantum field theory beyond the realm of particle physics nowadays form an extremely rich research area, dealing with quantum devices, cold atom gases, quantum spin chains, topological phases of matter and quantum systems out of equilibrium.

We plan:

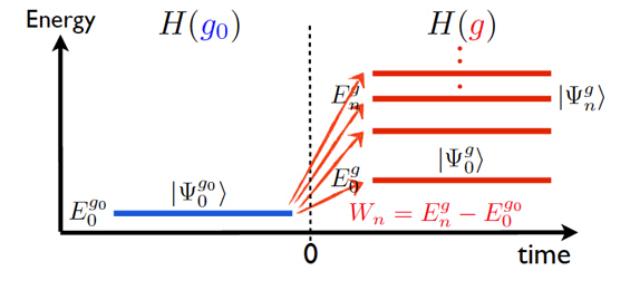
(1) to tackle important aspects of quantum field theory out of equilibrium and work out applications thereof (thermalization, exact solutions in quantum spin chains, generalized quantum hydrodynamics, computation of multipoint correlators);

(2) to understand the physical properties of entanglement (in particular its relation with symmetries and symmetry breaking patterns both in and out-of-equilibrium, the evolution of quantum information in open systems, the development of new protocols to measure the entanglement both in numerical simulations and experiments, the modelization of quantum computations, the use of the gauge/gravity correspondence also in connection with the information paradox in black holes);

(3) to study the emergence of new physical phenomena related to quantum integrability, its deformation and breaking (irrelevant perturbations and Hagedorn-type phase transitions, cold atoms in a trap, limit-shape phenomena, confinement of topological excitations, spectrum of neutral excitations, Majorana zero modes, massless renormalization group flows, many-body localization);

(4) to explore new universality classes of critical phenomena by using conformal invariance combined with conformal perturbation theory and very efficient numerical methods, such as the conformal bootstrap, truncated conformal space approach, DMRG, tensor networks, Monte Carlo and exact diagonalization techniques (applications to wetting phenomena, percolation, KPZ model, Potts model and Ising-like models above two dimensions, as well as to effective string theory);

(5) to investigate the properties of topological phases of matter (identification of corresponding topological field theories in three spatial dimensions, bosonization and dynamics of massless boundary excitations, and transport properties).

Keywords related to the topic of the proposal:

* Quantum field theories out of equilibrium

* Entanglement, quantum information and quantum computation

* Low-dimensional quantum field theory, integrable models and deformations

* Conformal invariance, conformal bootstrap and universality classes

* Topological phases of matter, field theories and bosonization