This project aims at making progress on a series of outstanding questions coming from statistical field theory and the area of quantum extended systems. Guidelines for the project are the exact and non-perturbative methods of quantum field theory, considerably refined in recent years thanks to developments in conformal field theories, exactly solvable lattice models and quantum integrable systems. A key feature of all these approaches is their ability to enlighten and account for strong coupling phenomena in quantum systems with infinite degrees of freedom. Applications of quantum field theory beyond the realm of high-energy physics nowadays form an extremely rich research area, dealing with quantum devices, cold atom gases, quantum spin chains, topological phases of matter and quantum systems out of equilibrium. We plan:

• to tackle important aspects of quantum field theory out of equilibrium and work out applications thereof (thermalization and its violation, the role of non-local conserved charges, the emergence of the Generalized Gibbs Ensemble, the exact computation of multi-point correlators, the manifestation of supersymmetry out of equilibrium, exact solutions of quantum spin chains);

• to enlighten significantly the universal properties of quantum entanglement (its proper measure for multiple partitions of the system, the spread of entanglement after a quantum quench, the topological information encoded in the entanglement spectrum);

• to reveal the properties of the new discovered topological phases of matter (identification of the relevant topological field theories in three dimensions, the role of boundary excitations and boundary states, transport properties, the use of the gauge/gravity correspondence);

• to explore new universality classes of critical phenomena by using conformal invariance combined with very efficient numerical methods, the Truncated Conformal Space Approach and the conformal bootstrap, as well as the finite-size techniques (applications to wetting phenomena, percolation, cold atoms in a trap, KPZ model, Potts model and Ising-like models above two dimensions);

• to study the emergence of new physical phenomena related to quantum integrability and its breaking (confinement of topological excitations, spectrum of neutral excitations, Majorana zero modes, massless Renormalization Group flows, many-body localization).

Keywords:
----------------------------
- Quantum field theories out of equilibrium
- Entanglement
- Topological quantum field theories
- Conformal invariance, phase transitions and universality classes
- Low-dimensional quantum field theory: integrability and its breaking

Brownian motion

Conformal map

Dimers

Lattice model

Plane partitions

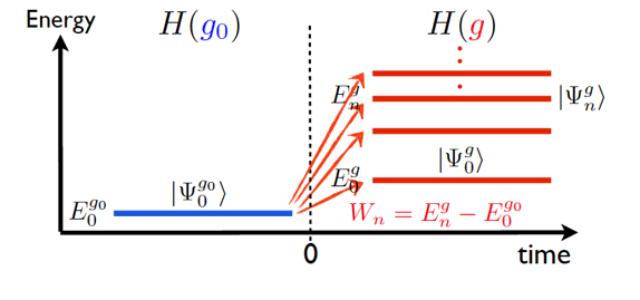Quantum quench

S-matrix bootstrap

Topological quantum computation