Abstract
This INFN Initiative gathers research activities in the
interdisciplinary area between Quantum Field Theory, Statistical
Physics and Condensed Matter Theory in low dimensions but not
only. The traditional methods of exactly solvable models, conformal
field theories and integrable systems have been considerably refined
in recent years and have remarkably enlarged their range of
application, thus leading to a very rich research area. A key feature
of these approaches is the ability of solving non-perturbative
many-body quantum phenomena that are being observed in recent
experiments of mesoscopic quantum devices, cold atom gases and
statistical systems out of equilibrium.
Among the developments that boosted the field, let us mention:
i) the increasing number of physical systems where quantum coherent
effects are dominant and give rise to new and astonishing behaviours;
ii) the growing interest in understanding the universal features of
entanglement and its future applications, among which the attempts at
realizing quantum computers;
iii) the possibility of extending the theoretical tools from low
dimensions to three space dimensions, as regarding topological effects
for example.
Present research projects can be grouped in three broad domains that
are deeply interconnected: (a) statistical properties of quantum
systems out of equilibrium, (b) measures of entanglement in quantum
extended systems, (c) new universality classes and new phases of
matter with topological features in two and three space dimensions.
Keywords:
----------------------------
- integrable quantum field theory
- conformal field theories and universality classes
- extended quantum systems out of equilibrium
- topological quantum field theory
- measures of quantum entanglement
 Brownian motion |
 Conformal map |
 Dimers |
 Lattice model |
 Plane partitions |
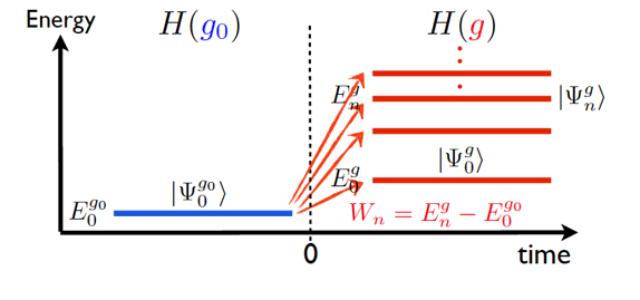 Quantum quench |
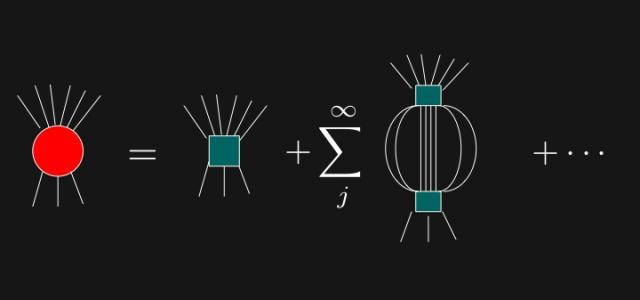 S-matrix bootstrap |
 Topological quantum computation |