Several highly non-trivial models in classical/quantum physics of wide applicative relevance (nuclear, optical, condensed matter and plasma physics, non-perturbative classical gravitation and quantum field theories, statistical models) share the mathematical property of Integrability. The integrable models are ubiquitary in many classical or quantum systems of applicative relevance, under suitable conditions and approximations.
The integrable, or quasi-integrable, models can be defined on continuous or discrete sets, as systems of PDEs, ODEs or Difference Equations. The investigation and the construction of integrable and quasi-integrable nonlinear equations allows for full analytic treatments.
Within the above general framework, the research of the MMNLP group
covers the following topics:
classification and construction of classes of integrable models by algebraic and geometric methods;
development of methods for solving initial-boundary value problems and construct exact solutions;
analysis of the singular behaviour of the solutions, in connection with the general singularity theory, the dispersive/dissipative regularization, shock formation, elliptic/hyperbolic transition regimes;
integrable partial/full discretization of differential systems;
development of local and nonlocal Hamiltonian and symplectic methods;
application of the theory of integrable nonlinear models to classical and quantum theories.
The theory of nonlinear partial, ordinary differential, and difference equations experienced a very intensive development during the last fifty years, particularly after the discovery of the Inverse Spectral Transform method (IST) in 1967, allowing one to solve the Cauchy problem for distinguished classes of nonlinear partial differential equations. Such a breakthrough enabled to construct wide classes of exact solutions, in particular solitons, that is space-localized time dependent waves which scatter elastically without emitting radiation. Their stability is due to the existence of families of infinitely many symmetries and conservation laws. Such properties can be analyzed in great details and allow to describe the asymptotic behaviour of the general solution.
Furthermore, Hamiltonian, bi-Hamiltonian and various other algebraic and geometrical structures can be associated with those systems. Thus, nonlinear integrable systems are investigated through a broad variety of methods and approaches, covering many branches of mathematical methods: complex analysis and generalized analytic function theory, functional analysis, symplectic geometry, Kac-Moody and Frobenius algebras, twistors, combinatorics, number theory, algebraic geometry, approximation theory and numerical algorithms.
|
|
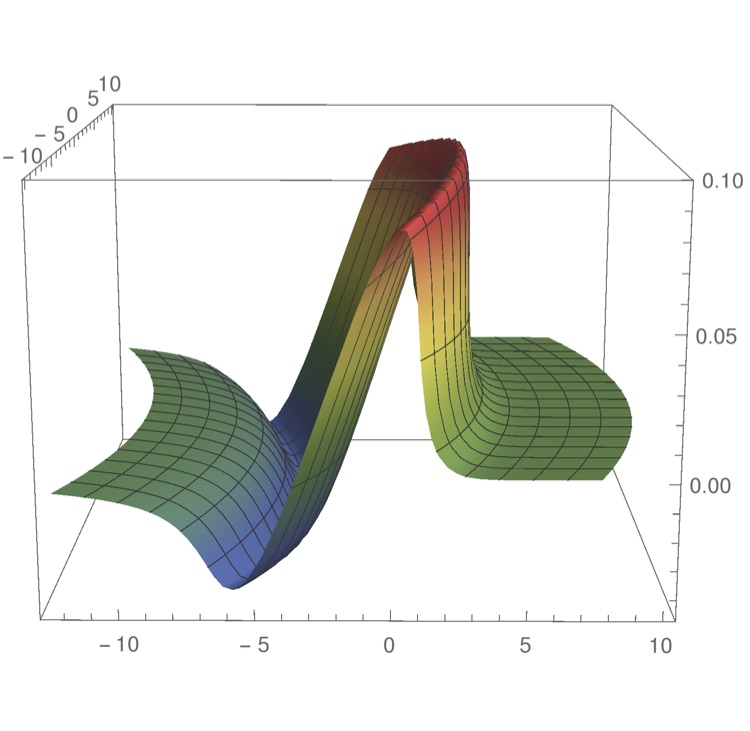
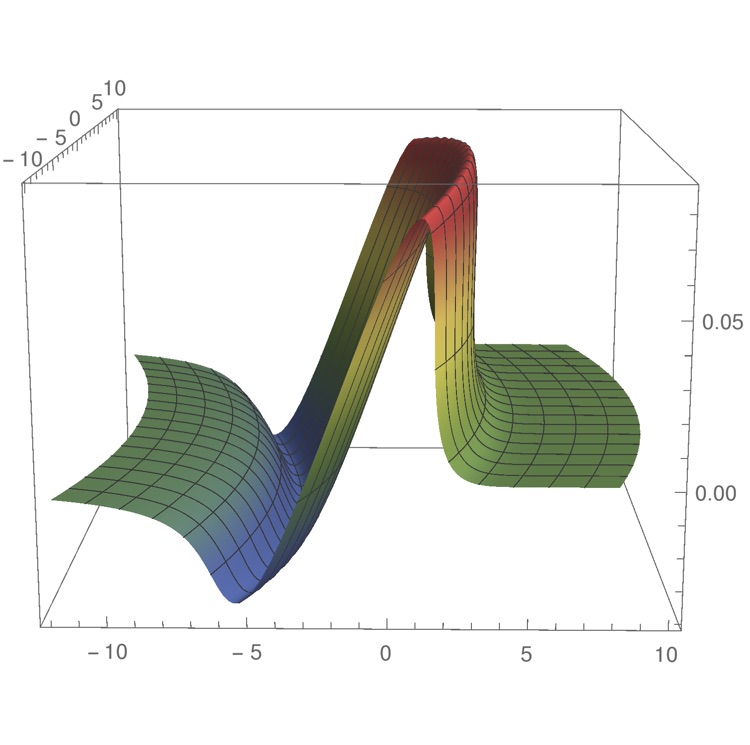
The plotting of the solution $u(x,y,t)\in\RR$ of the
dispersionless Kadomtsev - Petviashvili equation
$(u_t+uu_x)_x+u_{yy}=0$, describing the evolution of quasi - one
dimensional, weakly nonlinear waves in Nature, in the absence of
dispersion and dissipation, and integrable prototype model in the
description of wave breaking in multidimensions. The figures show
the asymptotic wave front at breaking and immediately after
breaking, as predicted by the theory.

The 3D plotting of $|u(x,t)|$, where $u(x,t)\in\CC$ is the solution of the Cauchy problem of the NLS equation $i u_t +u_{xx}+2 |u|^2 u=0$ for generic, $x$-periodic, small initial perturbations of the background solution $u_0(t)=e^{2 i t}$ (the simplest integrable model for the description of rogue waves in Nature, with applications in fluid dynamics, nonlinear optics, Bose - Einstein condensates, etc \dots ). The figure describes the exact recurrence of an infinite sequence of rogue waves, obtained through the numerical integration of the Cauchy problem with $2$ unstable modes, via the Split Step Fourier Method, in very good agreement with the theoretical predictions of the theory. The short axis is the $x$-axis and the long one is the $t$ axis.
|
|
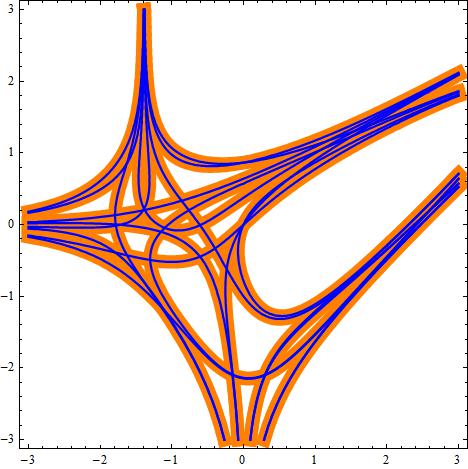
|
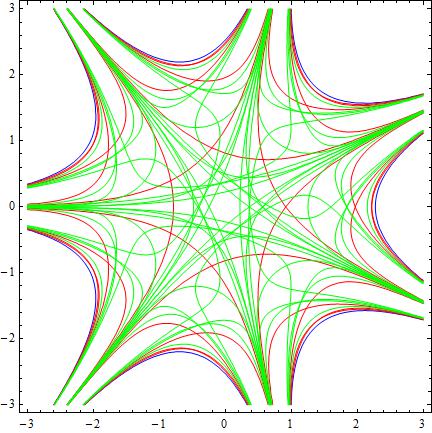
The loci of zeros Zsing for real-valued non-positively defined
partition functions Z for system of n variables. It is shown that
Zsing has a stratified structure and each stratum is a set of certain
hypersurfaces in Rn, known as statistical amoebas, arising in
considering the "tropical limit" of integrable systems.