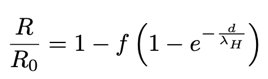Analisi dati dell’osservatorio Pierre Auger

da | Mag 16, 2020 | Laboratorio

? Esercizi interattivi  

L’Osservatorio Pierre Auger ha reso pubblici il 10% dei dati acquisiti finora.  

È possibile scaricare i dati direttamente dal sito della collaborazione Auger . 

Svolgendo i seguenti due esercizi, potrete scaricare dei piccoli file di dati, esplorarne il contenuto e analizzare i dati.  

Ogni esercizio viene svolto tramite un foglio di lavoro (notebook) messo a disposizione da Google Colab e utilizzando il linguaggio di programmazione Python. 

I dettagli dell’analisi sono indicati passo passo nel Google Colab.  

? Esercizio 1: Ricostruisci lo spettro dei raggi cosmici di energia estrema 

 Conoscendo l’energia degli sciami rivelati dall’Osservatorio e il numero di sciami raccolti in un certo intervallo di energia, possiamo calcolarne il flusso e costruire lo spettro dei raggi cosmici primari rappresentato in Fig. 1.  

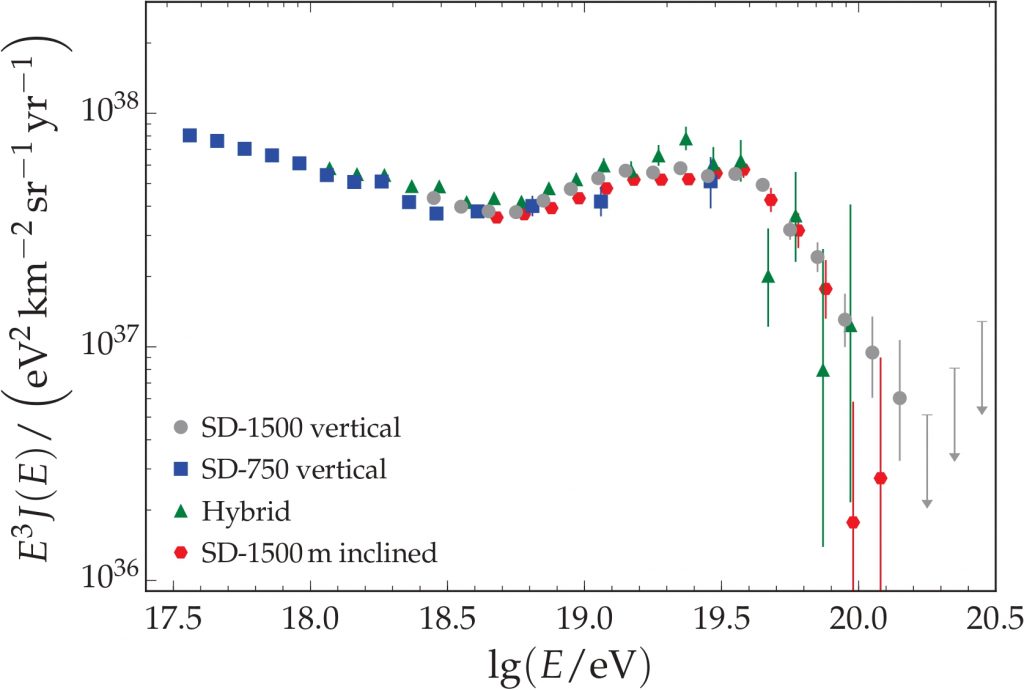
Fig. 1: spettro dei raggi cosmici di altissima energia misurato dall’Osservatorio Pierre Auger. Ciascuno degli spettri rappresentati in figura è stato ottenuto con diversi metodi e rivelatori dell’Osservatorio. Utilizzare più rivelatori e tecniche di misura diverse, permette di misurare lo spettro su un intervallo di energia più ampio. Gli intervalli di energia sono di 0.1 Log (E/eV). Ref. https://pos.sissa.it/301/486/pdf

Per ottenere il flusso, il numero di raggi cosmici va diviso per una quantità chiamata esposizione, che tiene conto del tempo in cui l’apparato è stato in presa dati, della superficie a disposizione per la misura e della porzione di cielo osservata. I punti in rosso di Fig. 1 rappresentano lo spettro ottenuto dai dati raccolti con il rivelatore di superficie dell’Osservatorio Auger. Lo spettro parte da un’energia di 1018.3 eV: sciami prodotti da raggi cosmici primari con questa energia possono essere rivelati dall’SD e ben ricostruiti.  

Analizzando i dati, ognuno di voi potrà contare i raggi cosmici rivelati in intervalli di 0.1 o 0.2 Log(E/eV) a partire da 18.3 log(E/eV) e costruire il proprio spettro.  

Cambiando la larghezza degli intervalli (bin) cambierà il numero di conteggi. Usando bin più stretti i conteggi all’interno di ognuno di essi diminuiranno e aumenteranno quindi le fluttuazioni statistiche. Verificalo svolgendo l’esercizio!  

Questa misura ha portato ad una delle più importanti scoperte dell’Osservatorio Auger, come l’esistenza di una soppressione nel flusso dei raggi cosmici ad altissima energia. Come si vede in Fig. 1, intorno a 1019.5 eV, è visibile una forte riduzione del numero di raggi cosmici. La Collaborazione continua a cercare la causa di questa soppressione.  

L’ipotesi più accreditata è che non esistano nell’Universo fenomeni astrofisici in grado di accelerare raggi cosmici fino ad energie che vadano oltre un certo limite. L’altra causa della soppressione potrebbe essere il cosiddetto effetto GZK, dovuto all’interazione dei raggi cosmici con una radiazione cosmica di fondo che pervade tutto l’Universo e che è stata originata all’epoca del Big Bang.  

Come vedi, abbiamo avuto tante importanti risposte fino ad ora, ma tante dobbiamo ancora cercarne. 

Vai all’esercizio 

? Esercizio 2: Costruisci la mappa galattica dei raggi cosmici di energia estrema 

Sappiamo che i raggi cosmici vengono prodotti da fenomeni astrofisici avvengono nell’Universo. Ma non sappiamo ancora non certezza quali sono queste “sorgenti” e dove si trovano. 

I raggi cosmici, essendo generalmente particelle cariche, risentono gli effetti dei campi magnetici galattici ed extra-galattici, pertanto le traiettorie che li portano fino a noi vengono deflesse lungo il cammino. Gli effetti del campo magnetico sulle traiettorie però si riducono all’aumentare dell’energia dei raggi cosmici. Studiando dunque la direzione di arrivo dei raggi cosmici di energia più elevata si può puntare la zona dello spazio da cui sono stati generati. 

In Fig.2, è rappresentato il flusso di particelle in coordinate galattiche (latitudine e longitudine). Il sistema di coordinate galattiche è un sistema di coordinate celesti centrato sulSole e allineato col centro della Via Lattea. L’“equatore galattico” è allineato con il piano galattico.  

L’Osservatorio Auger ha evidenziato che alcune galassie potrebbero essere più di altre sorgenti di raggi cosmici. Come si vede dalla mappa sottostante, si ha una densità maggiore di raggi cosmici in una zona di 13° intorno alla posizione di alcune galassie definite “starbust galaxy”, cioè galassie in cui è presente un’alta attività di formazione stellare. 

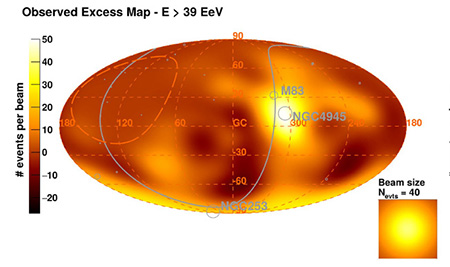Fig.2: Mappa delle direzioni di arrivo dei raggi cosmici di energia superiore a 6 Joule. Ref. Pierre Auger Observatory  www.auger.org

 Svolgendo l’esercizio, potrete divertirvi anche voi a costruire la vostra mappa galattica e a vedere cosa succede modificando l’energia dei raggi cosmici che disegnate e la risoluzione della mappa. 

Vai all’esercizio 

? Esercizio 3: Ricerca di eccessi di raggi cosmici di altissima energia. 

Il modo più evidente per cercare le sorgenti di raggi cosmici è certamente vedere da dove arrivano. Se puntano direttamente verso la posizione di uno dei “sospetti”, è la prova che stiamo cercando! Un problema fondamentale, però, è che i raggi cosmici, in quanto particelle cariche, vengono deviate dai campi magnetici e quindi non puntano direttamente alla direzione della loro sorgente, ma vengono “spalmati” intorno a questa (Fig.7).

Bisogna quindi andare a cercare regioni che mostrano un eccesso di raggi cosmici, ma questo può non essere facile: gli eventi che osserviamo sono pochi, e potrebbe succedere che per caso ne arrivino di più da una direzione che dall’altra… Affrontiamo questo problema con qualche base di statistica per poter definire quando un eccesso è significativo e quando invece è probabile che sia soltanto una cosiddetta fluttuazione statistica, ossia che i dati per caso simulino il segnale che cerchiamo.

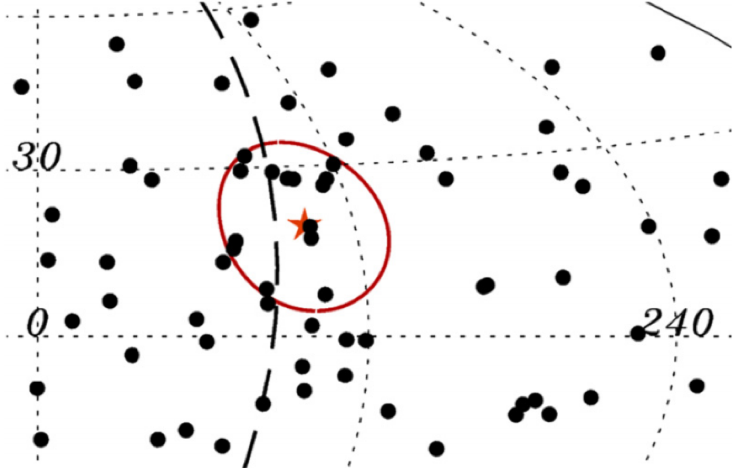
Fig.7: Particolare della mappa celeste dei raggi cosmici di energia estrema. La stella rappresenta la posizione di Centaurus A, la galassia attiva più vicina a noi, e il cerchio intorno ad essa indica la regione in cui è stato trovato un eccesso di raggi cosmici.

Vai all’esercizio

Misura della rate di muoni cosmici

da | Mag 14, 2020 | Laboratorio

Cosmic Ray Cube

Ai Laboratori Nazionali del Gran Sasso (LNGS) è stato progettato e realizzato un telescopio di raggi cosmici, ideato per essere utilizzato in eventi pubblici e didattici. Il telescopio, utilizzando le più innovative tecnologie che normalmente si impiegano negli esperimenti di fisica delle particelle, è in grado di visualizzare il passaggio di particelle contenute nello sciame di raggi cosmici che continuamente arrivano sul suolo terrestre. Lo strumento, chiamato Cosmic Rays Cube (CRC), grazie alla sua struttura compatta ed alla possibilità di essere alimentato a batteria è di facile portabilità e consente di misurare il flusso di particelle a varie altitudini, la loro distribuzione angolare, l’efficienza del rivelatore al variare di alcuni parametri di funzionamento.

Fig.1: Il Cosmic Ray Cube realizzato ai LNGS

Dispositivi analoghi o di dimensioni maggiori sono stati realizzati, in collaborazione con i LNGS, presso altri centri di ricerca e università internazionali (Laboratorio Subterraneo di Canfranc (LSC) in Spagna, New York University di Abu Dhabi (NYU-Abu Dhabi) e INFN Sezione Napoli).

Il rivelatore è in grado di rilevare la componente più penetrante dei raggi cosmici secondari, quella costituita dai muoni. Il muone è una particella che ha la stessa carica elettrica dell’elettrone, ma è circa 200 volte più pesante ed ha un tempo di vita media molto breve – 2,2 μs (vai al link).

La rivelazione del passaggio dei muoni all’interno del CRC avviene grazie all’utilizzo di una sofisticata tecnologia che impiega tre tipologie di rivelatori:

  • scintillatori plastici, in grado di convertire in luce l’energia rilasciata dall’interazione di una particella carica;
  • particolari fibre ottiche chiamate Wave Lenght Shifter (WLS) che raccolgono i segnali di luce e li convertono in luce di diversa lunghezza d’onda (dal blu al verde);
  • fotomoltiplicatori al Silicio (SiPM) in grado di convertire la luce raccolta dalla WLS in un segnale elettrico facilmente digitalizzabile.

Il CRC è inoltre dotato di LED che, grazie ad una sofisticata elettronica di acquisizione, si accendono al passaggio delle particelle, consentendo di seguire ad occhio nudo la traiettoria. Il rivelatore, pensato per essere un dispositivo portatile, è un cubo di lato 30cm, costituito da quattro moduli distanziati tra loro di 7 cm. Ogni modulo è costituito da 2 piani, ciascuno costituito da 6 bacchette scintillanti sovrapposte e posizionate ortogonalmente tra loro (Fig.2).

Fig.2: Uno dei quattro moduli costituenti il CRC: come si può vedere il modulo è costituito da due piani di bacchette scintillanti ortogonali tra loro.

All’interno di ciascuna bacchetta, di dimensioni 26 x 4 x 1 cm3, in un foro di circa 2 mm, è inserita una WLS, che convoglia la luce prodotta nello scintillatore verso il SiPM. Il segnale elettrico prodotto dal fotomoltiplicatore viene poi amplificato e digitalizzato.

Fig.3: Vista di una bacchetta scintillante al cui interno è inserita la WLS.

La configurazione geometrica delle bacchette scintillanti dà luogo, per ogni piano, ad una matrice di 36 pixel di 4×4 cm2, grazie alla quale è possibile individuare l’esatto punto di passaggio delle particelle.

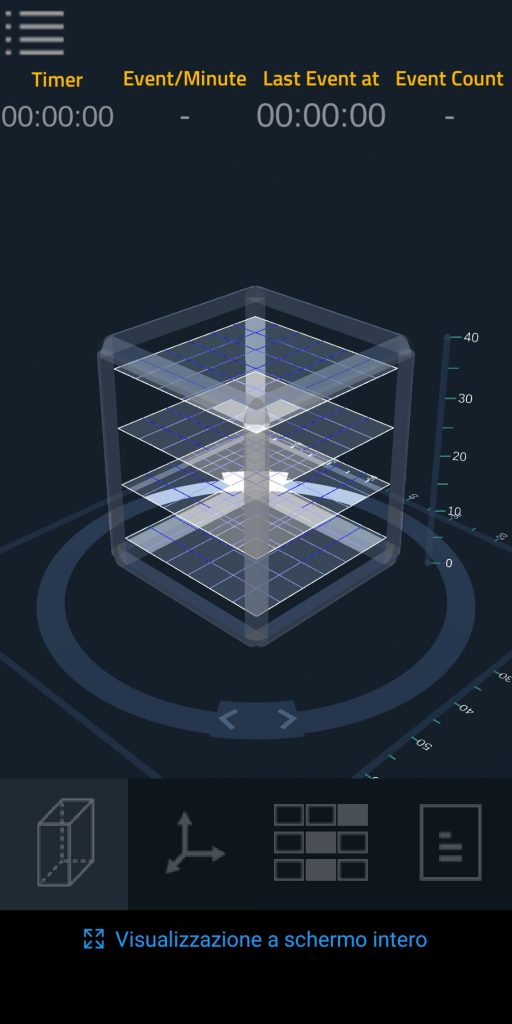
Fig.4: Rendering del CRC e dei 4 moduli che permettono di ricostruire la traiettoria della traccia.

Decodifica dei dati

Ai Laboratori del Gran Sasso è stata sviluppata, in collaborazione con professionisti del settore, l’App “Cosmic Rays Live”, scaricabile da qualsiasi smartphone, sul quale possono essere salvati interi set di dati raccolti dal CRC. Con sistema Android o iOS i dati vengono automaticamente salvati sul cellulare ogniqualvolta ci si collega ad uno dei siti dove sono dislocati i telescopi (Laboratori Nazionali del Gran Sasso, Laboratorio Sotterraneo di Canfranc in Spagna, New York University di Abu Dhabi e Monte Soratte). Seguendo il percorso “File Manager” (scaricare questa cartella da Play Store se non la si trova di default sul proprio smartphone), quindi cartella “Download”, quindi cartella “CRC” si arriva a visualizzare un set di dati composto come quello indicato in Fig.5.

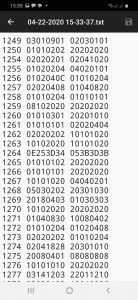Fig.5: Dati raccolti dal CRC e visualizzabili attraverso l’app Cosmic Rays Live.

Nella prima colonna troviamo il numero di evento, nella seconda e terza colonna ci sono due stringhe di caratteri in formato esadecimale, che opportunamente decodificati, daranno i valori delle coordinate nell’asse X e nell’asse Y per i 4 piani. Per definire il passaggio della particella nelle bacchette scintillanti colpite nelle due viste del rivelatore, bisogna quindi effettuare la decodifica secondo i seguenti passaggi:

1) Consideriamo l’evento 1254 indicato nella Fig.5 e trasformiamo ciascuna coppia di numeri esadecimali della prima stringa (01010202) in numeri binari a 6 cifre utilizzando Excel. Otterremo la seguente conversione hex-binario:

  • 02 –>000010
  • 02–>000010
  • 02–>000010
  • 01–>000001

2) Analogamente trasformiamo ciascuna coppia di numeri esadecimali della seconda stringa (02041020) in numeri binari a 6 cifre con Excel:

  • 02–>000010
  • 04–>000100
  • 10–>010000
  • 20–>100000

3) Mettiamo questi numeri binari in una tabella di 4 righe e 6 colonne e proviamo a visualizzare la traiettoria della particella nella due viste X e Y del telescopio. Gli “1” indicano che la bacchetta di scintillatore è stata colpita da una particella, mentre gli “0” indicano che quella bacchetta non è stata colpita.

Nel caso dell’evento1254 abbiamo:

  • 02020201 sul piano XZ che decodificato diventa

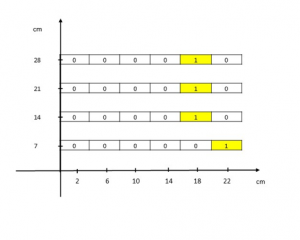
Fig.6: Visualizzazione schematica delle bacchette colpite dalla particella su ogni piano, nella vista X.

  • 02041020, sul piano YZ, diventa

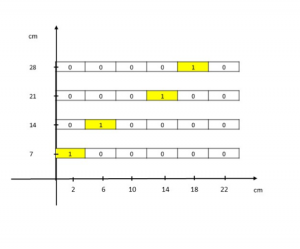
Fig.7: Visualizzazione schematica delle bacchette colpite dalla particella su ogni piano, nella vista Y.

Ricostruzione della traccia

A partire da queste informazioni, conoscendo la larghezza delle strip (4 cm) e la distanza tra i vari piani (7 cm) è possibile determinare i valori delle x e delle y in funzione dei piani colpiti. Riportiamo in due tabelle i valori delle x e delle y in funzione dei piani del rivelatore:

Z [cm]  X [cm] 
28  18 
21  18 
14  18 
7  22 
Z [cm]  Y [cm] 
28  18 
21  14 
14  6 
7  2 

Utilizziamo Excel per riportare questi dati su due grafici e determinare le linea di tendenza dell’andamento dei punti, assumendo una relazione lineare tra i valori z e x (oppure z e y): utilizziamo quindi un modello che si chiama della regressione lineare che ipotizza una funzione del tipo

X = mx Z + qx

in cui

  • X=variabile dipendente da Z
  • Z=variabile indipendente
  • qx=termine costante che rappresenta l’intercetta della retta
  • mx= coefficiente di relazione tra X e Z

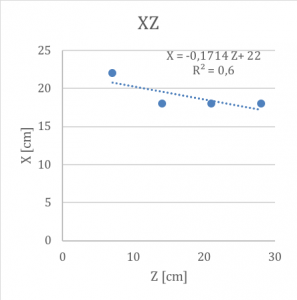
Fig.8: Determinazione linea di tendenza sul piano XZ utilizzando Excel.

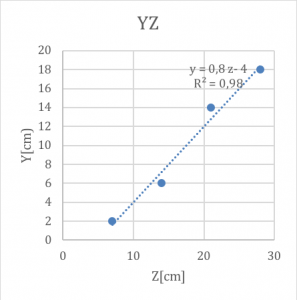
Fig.9: Determinazione linea di tendenza sul piano YZ utilizzando Excel.

Disegniamo la retta della funzione trovata X(Z) sul piano XZ dove però sull’asse dell’ascisse sono riportati i valori di X e su quello delle ordinate i valori di Z: definiamo quindi i punti P1 (X(0), 0) e P2 (X (h), h) con h altezza totale del cubo che permetteranno di ricostruire la retta con excel.

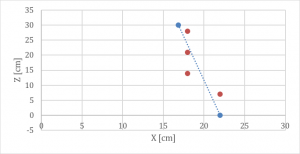
Fig.10: Linea di tendenza trovata X(Z), riportata su un grafico dove sono stati scambiati gli assi: confrontare con Fig.6.

Analogamente per il piano YZ otteniamo:

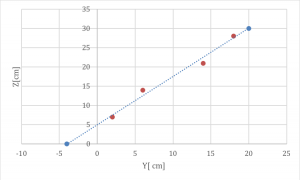
Fig.11: Linea di tendenza trovata Y(Z), riportata su un grafico dove sono stati scambiati gli assi: confrontare con Fig.7.

Le linee di tendenza dei due grafici rappresentano le proiezioni della traiettoria del muone sul piano ZX e ZY.

Per individuare la traiettoria 3D della particella all’interno del cubo, una volta determinate le funzioni x = mx * z + qx e y = my * z + qy, da queste è possibile individuare il vettore “direttore” 3D da cui si possono determinare gli angoli theta e phi.

Si può procedere in questo modo:

  1. Si fanno passare le due rette individuate per l’origine degli assi: per fare questo si pongono i termini noti uguale a zero. Si ottengono quindi le due rette

x = mx * z e y = my * z

parallele a

x = mx * z + qx e y = my * z + qy

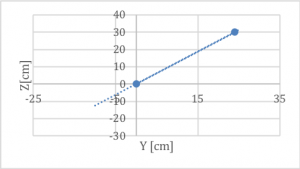
Fig.12: Retta Y(Z) passante per origine

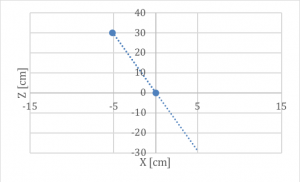
Fig.13: Retta X(Z) passante per origine.

Scegliendo per z il valore 1 ottengo la terna per il vettore direttore che chiamo

v = (vx, vy, vz) = (mx, my, 1)

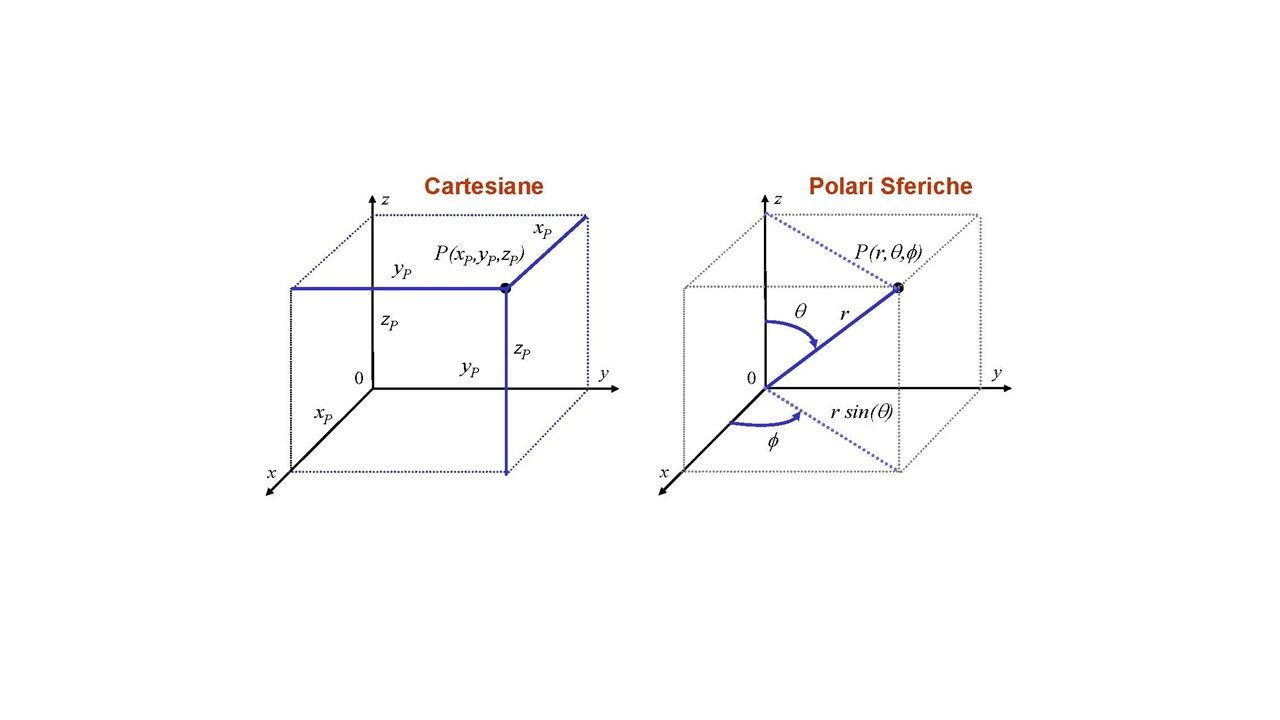Fig.14: Sistemi di cartesiane 3d cartesiane e polari sferiche.

Passando dal sistema di coordinate 3d cartesiane a quelle polari sferiche (Fig.14), si ricavano gli angoli θ e φ a partire dai coefficienti mx e my. Utilizzeremo le seguenti formule

θ= arccos(vz / v),

dove v = √(vx2 + vy2 + vz2)

in cui l’arctan2(y,x) è l’arcotangente, che tramite identità trigonometrica, elimina l’ambiguità della periodicità a 180 della tangente sul piano x, y, restituento phi tra -π a +π. I valori trovati sono riportati in radianti e possono essere convertiti in gradi sia utilizzando la funzione “gradi” di excel che moltiplicando i valori ottenuti per (180/π).

Otteniamo quindi:

Tetha = 39,28°

Phi = -12,09°

A questo punto è possibile ricostruire la traiettoria del muone all’interno del CRC (si può fare utilizzando GEOGEBRA).

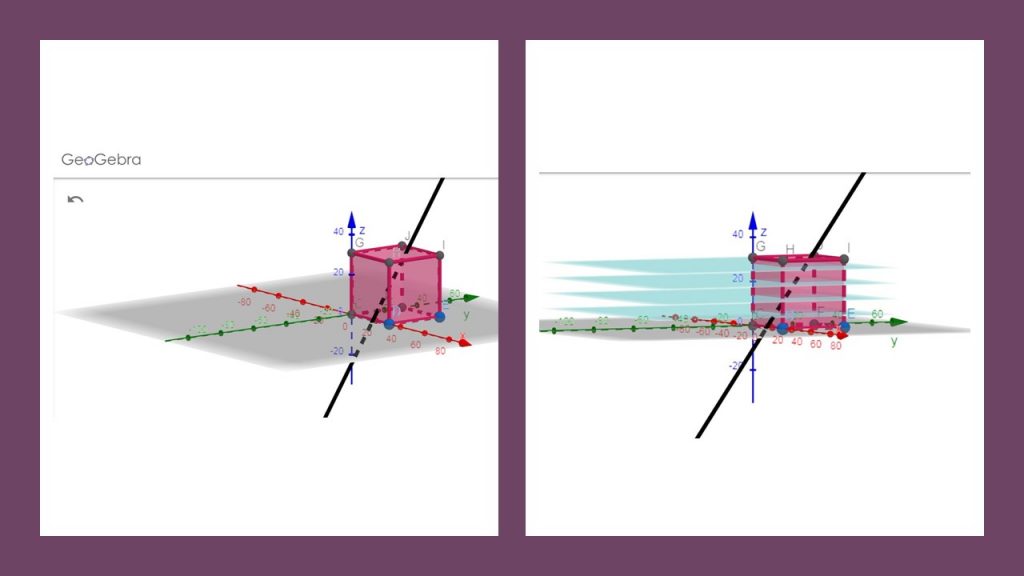
Fig.15: Ricostruzione traccia 3D con Geogebra.

Il foglio di lavoro excel al link riporta la ricostruzione descritta.

Ricostruzione delle tracce con App “Cosmic Rays Live” 

Quello che sinora abbiamo ricavato con semplici passaggi matematici viene invece calcolato automaticamente dall’App. Collegandosi ad uno dei siti indicati nell’App dove sono dislocati i CRC, è possibile vedere in tempo reale il passaggio dei muoni all’interno dei rivelatori grazie ad un dedicato programma di grafica in 3D. In essa sono inoltre riportate le viste X e Y, gli istogrammi dei pixel colpiti relativi al set di dati raccolto e il numero di conteggi per canale e di ciascun piano (Fig. 16).

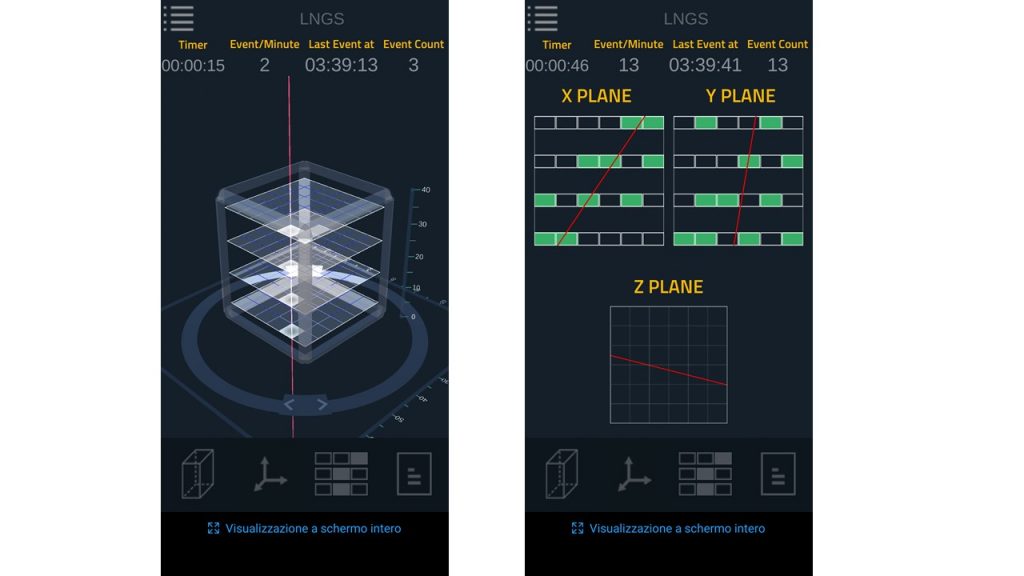
Fig.16: Ricostruzione traccia dell’App Cosmic Rays Live.

E’ interessante notare che un telescopio di dimensioni maggiori fatto da 10 piani e 10 canali, progettato e realizzato ai LNGS e gestito dalla Sezione INFN di Napoli, è in acquisizione nella stazione Toledo della metropolitana di Napoli.  L’analisi dei dati di questo telescopio è riportata nel percorso Misura della distribuzione angolare dei muoni.

Misura della distribuzione angolare dei muoni

da | Mag 14, 2020 | Laboratorio

Il telescopio per muoni cosmici della metropolitana di Toledo a Napoli

Il percorso ci porterà alla scoperta del rivelatore istallato nel 2014 nella stazione di Toledo (Fig.1), la più bella stazione metropolitana d’Europa! Guarda il Video

Nel percorso “Raggi Cosmici” Abbiamo imparato molto sul muone e come si può rivelare. In questo percorso vedremo come un telescopio installato sotto 40 m di roccia può rivelare queste particelle che hanno una massa 200 volte quella dell’elettrone e che vivono solo 2.2 us. Il telescopio descritto in questo percorso è simile al Cosmic Ray Cube (CRC), solo che è costituito da 10 piani rispetto ai 4 del CRC.

Fig.1: Il telescopio installato nella stazione Toledo della metropolitana di Napoli, a destra è visibile anche il Totem multimediale che permette, tra l’altro, di registrare i dati e di renderli accessibili in rete.

I 10 piani del telescopio sono realizzati da bacchette di materiale scintillante plastico che emette un debole impulso di luce quando è attraversato da particelle cariche come i muoni. Le barre sono disposte ortogonalmente tra loro sul piano orizzontale (direzione x e y) ed hanno ciascuna dimensioni di 4 x 1 x 40 cm3. Ogni barra è otticamente accoppiata con una fibra ottica ad un fotomoltiplicatore a silicio (Silicon Photomultiplier – SiPM) che assorbe la luce emessa dallo scintillatore e la trasforma in una corrente elettrica che, attraverso una scheda di elettronica, permette l’accensione dei 200 LED per la ricostruzione in 3D dei muoni che attraversano il rivelatore. Quando un muone attraversa il telescopio, viene quindi visualizzata una traccia luminosa come nella Fig.1. Inoltre, il telescopio è accoppiato ad un Totem touchscreen multimediale che permette l’acquisizione dei dati del telescopio tramite una connessione seriale, la ricostruzione della direzione di provenienza dei muoni e la visualizzazione della loro traccia sullo schermo (Fig.2).

Fig.2: Ricostruzione della traccia di un muone rivelato dal telescopio come visualizzata  sul Totem.

Richiedendo che almeno su sei piani del telescopio ci sia un LED acceso, si ottiene una rate di 4 eventi al minuto.

Ascolta la descrizione del telescopio dalla voce di chi lo ha progettato e costruito, insieme ai colleghi dei Laboratori Nazionali del Gran Sasso e della Sezione INFN di Napoli. http://people.na.infn.it/~totem/Video/Attanasio.htm

Decodifica Tracce

I dati acquisiti dal telescopio possono essere scaricati dal sito http://people.na.infn.it/~totem.

I file “Muoni_Eventi_anno_mese_giorno.txt” contengono i dati “raw”, mentre i file “Muoni_Orario_anno_mese_giorno.txt” contengono i dati ricostruiti per ciascuna faccia del telescopio. Le quattro colonne di questi ultimi file rappresentano: numero identificativo dell’evento, data di acquisizione e angolo che la traccia forma con la verticale rispettivamente nella faccia XZ e YZ (theta_x e theta_y).

Un evento “raw” è rappresentato nel seguente modo (Fig.3):

STF337

00000100200F00C018030020040180

008018010018018018010030010010

ST indica che c’è un nuovo evento, mentre F337 il numero di evento espresso in esadecimale. Le due righe successive sono due stringhe esadecimale che, come per il CRC, ci permettono di ricostruire quali bacchette di scintillatore sono state colpite dal passaggio del muone e, quindi, quali LED si sono accesi sulle due facce del telescopio. La prima stringa rappresenta la vista XZ, vista MASTER, mentre la seconda la vista YZ, vista SLAVE. Ogni stringa ha 30 caratteri, ogni 3 caratteri indicano un piano. Trasformandoli in binario otteniamo 12 canali dei quali i primi due non vanno considerati. In particolare, per il telescopio di Toledo i primi 3 caratteri esadecimali danno l’informazione dei canali accesi (“1”), relativi al piano più basso e così via. Si tenga presente che una stringa di tutti 0, in alcuni casi, può indicare che quel piano, sebbene sia stato interessato dal passaggio della particella, non ha “acceso” alcuna bacchetta di scintillatore e questo in genere accade per sola inefficienza di quello scintillatore o del sistema scintillatore-WLS-SiPM.

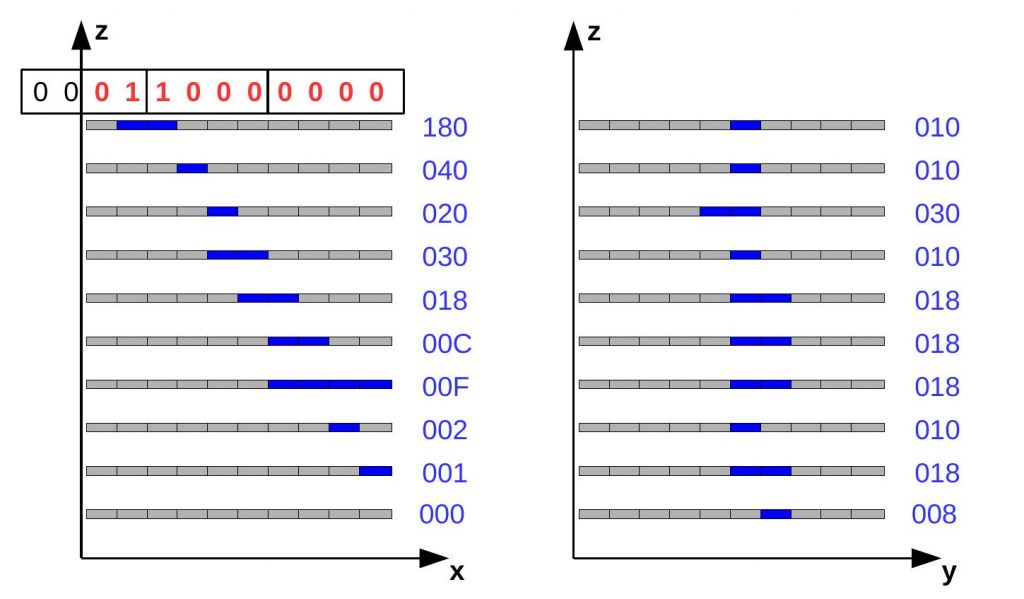
Fig.3: Decodifica dei dati Raw per ricostruire la traccia dei muoni.

Come ricostruire le due rette che indicano il passaggio del muone sulle due facce a partire dai dati raw e la retta nello spazio identificata dagli angoli theta e phi è spiegato nel percorso Misura della rate di muoni cosmici.

In questo percorso ti proponiamo i seguenti:

? Esercizi interattivi

Partiremo dai dati contenuti nei file “Muoni_Orario_anno_mese_giorno.txt”, che, come abbiamo detto, contengono gli angoli che la traccia forma con la verticale rispettivamente nella faccia XZ e YZ. Questi identificano la direzione nel piano del muone che attraversa il telescopio, in quanto la loro tangente rappresenta il coefficiente angolare della retta/traccia. Scritte le rette nei due piani, possiamo ricavare theta e phi che descrivono la retta nello spazio.

Ogni esercizio viene svolto tramite un foglio di lavoro (notebook) messo a disposizione da Google Colab e utilizzando il linguaggio di programmazione Python.

I dettagli dell’analisi sono indicati passo passo nel Google Colab.

Quando si analizza un numero elevato di dati discreti, al fine di dare un senso all’analisi dei dati stessi, si rende necessaria la suddivisione in intervalli di valori che comprendono tutti i dati che vi appartengono. Si suddividono gli eventi dell’arrivo dei muoni in base all’inclinazione che hanno rispetto una determinata direzione, si creano così degli intervalli in cui andiamo a contare tutti gli eventi che hanno un angolo compreso tra i due estremi dell’intervallo.

Quando abbiamo un insieme di dati ed andiamo a contare quante volte essi si presentano all’interno di ogni intervallo che abbiamo definito, parliamo di distribuzione di frequenze cioè una funzione che può essere rappresentata elencando tutte le coppie ordinate in una tabella avente come colonne l’intervallo di valori considerato e la frequenza assoluta (il numero di casi che si contano nell’intervallo). Il modo più semplice per elaborare un insieme di dati statistici e di trarre le prime osservazioni sull’andamento del fenomeno che si sta osservando è quello di rappresentarli graficamente. Generalmente il modello di rappresentazione più utilizzata per i fenomeni fisici osservati è quello dell’istogramma che è un particolare diagramma cartesiano che ha sulle ascisse valori discreti xi o intervalli di valori (che chiamiamo bin), sulle ordinate l’altezza della colonna rappresentante il numero delle frequenze in funzione dei valori presi in considerazione.

Introduciamo dunque due termini tecnici che spesso saranno utilizzati nelle attività di questo percorso che sono “bin” (o binning) e “fit” (o fitting). Per costruire un istogramma bisogna innanzitutto considerare il numero totale di dati, bisogna scegliere il binning ovvero la divisione del dominio della variabile sulle ascisse, cioè si deve definire il numero di intervalli e la loro ampiezza, infine si devono conteggiare i dati da associare ai singoli bin (cioè contare il numero di dati che cade in ogni singolo intervallo).

Dopo aver trasformato i dati sperimentali raccolti in un istogramma si cerca di ricavare una curva che sia in grado di “raccontare” meglio il comportamento dei dati. Un metodo tipico è quello del “best fit” ossia la ricerca di una curva che abbia come caratteristica essenziale che la curva approssimante si avvicini il più possibile ai punti.

Per scegliere la curva di fitting si deve valutare quale funzione matematica potrebbe essere più rappresentativa per l’analisi del fenomeno. Possiamo immaginare una regressione di tipo lineare o polinomiale o esponenziale o sinusoidale … o la “distribuzione normale” (o gaussiana). Il nome “normale” deriva dalla convinzione che molti fenomeni fisici e biologici si distribuiscono con frequenze più elevate nei valori centrali e con frequenze progressivamente minori verso gli estremi della variabile. Questa distribuzione è caratteristica dei fenomeni casuali. L’equazione della funzione normale è la seguente:

Si tratta di una curva dalla classica forma a campana che ha un massimo nel valore medio dei valori misurati e può essere più o meno stretta a seconda della dispersione dei valori attorno alla media; la dispersione si misura con la deviazione standard.

? Esercizio 1: 

Puoi scaricare i dati del telescopio, convertirli in una tabella e infine, dopo un po’ di elaborazione, costruire degli istogrammi relativi alle distribuzioni delle direzioni di arrivo dei muoni. Potrai modificare interattivamente il numero dei bin di ciascun istogramma e verificarne l’effetto nella visualizzazione dei dati. Diversi aspetti fisici andrebbero considerati per spiegare la forma delle distribuzioni ottenute, se sei curioso contattaci e approfondiremo insieme questi aspetti.

Vai all’esercizio: https://colab.research.google.com/drive/1mhNjQ6xpcp7L23RL9PABGIyFpEurAzvE?usp=sharing

 

 

? Esercizio 2:  Puoi trovare quale tra le curve proposte meglio si adatta alle distribuzioni trovate tramite la procedura di fit. Potrai scegliere tra due diverse funzioni polinomiali, la gaussiana o la gaussiana asimmetrica. Di ciascuna potrai variare i parametri iniziali e scoprire come variano dopo il fit.

Vai all’esercizio: https://colab.research.google.com/drive/1gRwq45HP0QCPKbbRaS_QiDhaduUu4H5r?usp=sharing

Misura dei muoni in funzione dell’angolo di Zenith

da | Mag 14, 2020 | Laboratorio

Le misure che descriviamo in questa sezione e che rendiamo disponibili per l’analisi dati sono state eseguite durante l’INTERNATIONAL COSMIC DAY (ICD). L’ICD è un progetto internazionale per gli Istituti Superiori organizzato dall’Istituto Nazionale di Fisica Nucleare (https://web.infn.it/OCRA/international-cosmic-day/) in collaborazione con DESY Accelerator Laboratory (Amburgo) e con altri Laboratori di Fisica e Istituti in tutto il mondo. Durante la giornata dedicata ai raggi cosmici gli studenti entrano in contatto con l’attività di ricerca in fisica, portano a termine un piccolo esperimento sui raggi cosmici, analizzano i dati, confrontano i propri risultati con gli altri gruppi collegati da altre università o centri di ricerca nel mondo, lavorano per un giorno come in una collaborazione internazionale e pubblicano i risultati.

Cosa dobbiamo misurare?

I raggi cosmici primari (come spiegato qui) non riescono a raggiungere la superficie terrestre perché interagiscono (si scontrano) con gli atomi dell’atmosfera creando una cascata di particelle secondarie. Questi sciami di particelle secondarie durano pochi miliardesimi di secondo e, una volta arrivati a terra, possono coprire un’area di diversi chilometri quadrati. Tra le particelle cariche che arrivano a terra, i muoni sono quelli più facilmente misurabili. Nonostante risultino invisibili all’occhio umano, il metodo usato dai ricercatori, per evidenziarne il passaggio, consiste nel farli interagire con la materia sensibile (particolari materiali che diano un segnale elettrico o luminoso una volta che vengono attraversati da queste particelle). La registrazione di questi fenomeni fornisce ai ricercatori informazioni sul passaggio delle particelle e dell’energia che hanno rilasciato. Questa strumentazione prende il nome di rivelatore (“detector” in inglese). Il rivelatore utilizzato in questa esperienza è il CosmicRayCube (CRC), per una descrizione dettagliata del rivelatore usato per queste misure vi rimandiamo al link: CRC. In sintesi il rivelatore è fatto da 4 piani di rivelazione messi in coincidenza.

Muoni

Ricapitoliamo velocemente quali sono le caratteristiche delle particelle che andremo ad osservare, i muoni:

  • sono simili agli elettroni, ma hanno una massa 200 volte maggiore;
  • attraversano materiali poco densi (come le pareti degli edifici e i nostri corpi) perdendo poca energia;
  • ogni minuto veniamo attraversati da centinaia di muoni, essi contribuiscono alla dose di radioattività naturale a cui siamo soggetti;
  • nonostante abbiano una vita media di 2.2 milionesimi di secondo, arrivano fino alla superficie della terra e si fermano dopo aver attraversato decine di metri sottoterra in strati di roccia.

Misura del flusso di raggi cosmici in funzione dell’angolo di zenit

Il flusso di muoni a terra non è uniformemente distribuito. Analizzando le direzioni di arrivo di queste particelle in funzione dell’angolo che esse formano con lo zenit locale, si scopre che il flusso massimo si ha per θ=0° ossia per particelle che arrivano perpendicolarmente alla superficie terrestre. Il flusso diminuisce continuamente all’aumentare dell’angolo tra la direzione di incidenza e lo zenit. A 90° il flusso è minimo. Come è spiegato in Review of Particle Data (1), la distribuzione dei valori misurati può essere descritta usando una funzione cos².

Diversi effetti sono responsabili di questo comportamento, tra questi, il cammino percorso dalle particelle cosmiche attraverso l’atmosfera.

I muoni, prodotti a 15 km di altezza nell’atmosfera, sono il prodotto di decadimenti di altre particelle come pioni e kaoni prodotti nell’interazione tra i raggi cosmici primari e gli atomi nell’atmosfera. Come si vede dal link, facendo uso della sola interpretazione fisica classica, queste particelle non potrebbero arrivare a terra (visto che la loro vita è di solo 2,2 μs), ma l’interpretazione fornita da Einstein con la relatività speciale ci spiega come fanno i muoni, che si muovono a velocità prossime a quelle della luce, a percorrere tutta l’atmosfera fino ad arrivare alla superficie terrestre. Quindi ci aspettiamo di vedere solo i muoni che riescono a percorrere lo strato di atmosfera prima del loro decadimento.

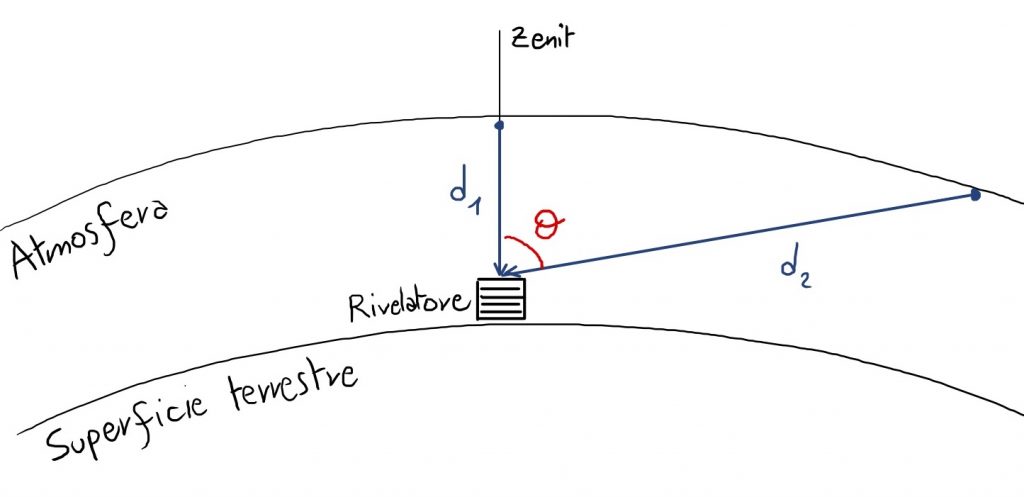
Fig.1: Rappresentazione dei cammini (d1 e d2) effettuati da due muoni prodotti in atmosfera e diretti verso il rivelatore posto sulla superficie terrestre.

Con riferimento alla Fig.1,  i muoni che arrivano perpendicolarmente alla superficie terrestre (arrivano lungo la direzione dello zenit locale), percorrono meno strada in atmosfera, mentre, per angoli di incidenza elevati, angolo theta rispetto allo zenit, la distanza viene estesa. Con un angolo di incidenza di 90°, la distanza che il muone deve percorrere attraverso l’atmosfera fino alla superficie della terra è di circa 400 km (anziché 15 km). Solo pochi alti picchi di energia riescono a coprire questo percorso. In conclusione, maggiore è l’angolo dallo zenit, maggiore è la distanza percorsa, maggiore sarà la probabilità che i muoni decadano prima di raggiungere la superficie terrestre e quindi il flusso sarà minore.

LA TECNICA SPERIMENTALE

Il numero di muoni (conteggi, C) incidenti nel rivelatore in un intervallo di tempo (T) prende il nome di rate (R=C/T) espresso in particelle al secondo. La presa dati risulta quindi sintetizzata in questo modo:

  • Prendo dati per un tempo T
  • Conto il numero di particelle registrate C
  • Calcolo il rate R delle particelle come: R = C / T (part/sec)

Esempio:

Prendo dati per 100 secondi (T=100 secondi)

Lo strumento registra C=1000 particelle

R= C / T = 1000/100 = 10 particelle/secondo

Fissato un tempo, misurare la dipendenza dei conteggi dall’angolo di inclinazione (Fig.2).

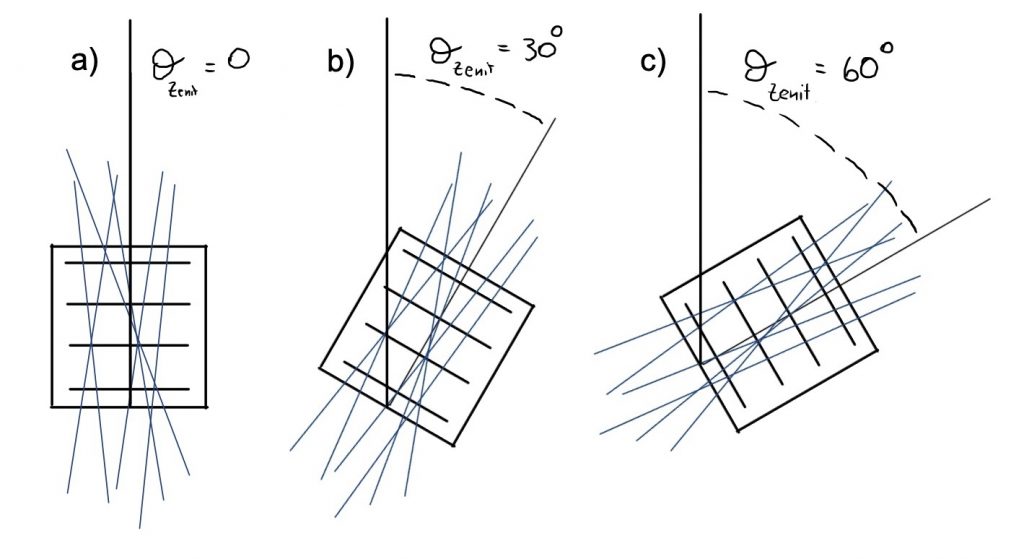
Fig. 2: Rappresentazione della configurazione sperimentale, il rivelatore, inizialmente posizionato con l’asse parallelo allo zenit locale (a), viene inclinato ad angoli via via sempre maggiori: 30° (b), 60° (c) fino a posizionarlo orizzontalmente.

Raccolta dati

Per questa parte dell’esperienza è conveniente utilizzare un foglio di calcolo, puoi usare quello che preferisci o che usi già, per esempio Excel, Calc o un foglio di lavoro google.

Noi li abbiamo inseriti in un foglio di lavoro google che trovi in: shorturl.at/kvEO0

Quando sono presenti più misure dello stesso angolo, come puoi stimare la misura? La migliore stima del valore vero è la media aritmetica dei valori ottenuti nelle varie misure. Tieni conto che alcune misure di C potrebbero riferirsi a tempi di acquisizione diversi (l’intervallo di conteggio è indicato tra parentesi nella legenda).

Riempi una tabella con i dati (θ, C)!

Ogni misura sperimentale di una grandezza è affetta da errori sistematici e statistici. Per quanto riguarda la stima dell’errore delle singole misure ci concentreremo sull’aspetto statistico. Possibili spunti per individuare le sorgenti di errori sistematici sono forniti al termine dell’esperienza. Noi misuriamo il numero di raggi cosmici che provengono dallo spazio nello stesso intervallo di tempo. Se ripetiamo la misura diverse volte, non otteniamo sempre lo stesso risultato ma possiamo fare delle considerazioni di carattere statistico cioè possiamo dire qual è la probabilità di avere un certo risultato. La distribuzione di probabilità che descrive, con buona approssimazione, i fenomeni di conteggio di raggi cosmici è la distribuzione di POISSON. La distribuzione di probabilità di Poisson si applica quando si ha a che fare con eventi rari riferiti ad uno specifico intervallo di tempo. L’errore statistico associato a questo tipo di distribuzione è √C, dove C è il numero di eventi per ogni misura. Siccome stiamo analizzando il rate delle particelle, l’errore relativo a questa quantità deriva dalla propagazione degli errori dividendo, quindi, l’errore del numero di conteggi (√C) per il tempo T. Se volessimo avere errori relativi confrontabili per ogni misura cosa avremmo potuto fare durante la presa dati? (Partecipate all’ICD per conoscere la risposta!)

ANALISI DEI DATI

  1. Calcolare il rate dei muoni: R = C / T (part/sec) per ciascun angolo e associare il relativo errore statistico
  2. Disegnare il grafico: rate (asse y) in funzione dell’inclinazione theta (asse x)
  3. Ci aspettiamo una dipendenza da cos2θ. Come si confronta questa previsione coi tuoi dati?
  4. Può essere pratico calcolare grandezze come cos2θ. Prova a rifare il grafico in funzione di cos2θ e verifica che i dati sono approssimabili ad una retta. Calcola il coefficiente angolare della retta usando la regressione lineare.
  5. Come riportato nell’articolo Review of Particle Data (1), l’andamento del cos2θ è riferito all’intensità (I = R/(G*ε) ) dei raggi cosmici e non al rate. Ricordiamo che G è il fattore geometrico di accettanza (espressa in m2sr) ed ε rappresenta le efficienze del rivelatore (si veda il link ); entrambi G e ε sono proprietà intrinseche della strumentazione utilizzata. Sapresti spiegare cosa sarebbe cambiato se avessimo utilizzato l’intensità dei muoni anziché il rate?
  6. Cosa succederebbe se disegnassi il rapporto di R(θ)/R0 e I(θ)/I0 (sull’asse y) in funzione dell’angolo θ (asse x)? R0 e I0 sono rispettivamente il rate e l’intensità dei muoni che arrivano verticali (θ=0).

Riflettiamo sulla “geometria del rivelatore”

Con riferimento alla Fig.3, come pensi possa variare il rate/intensità delle particelle osservate modificando la distanza tra i piani del rivelatore dalla configurazione (a) alla configurazione (b)? Cosa succede invece se si passa da (a) a (c)?

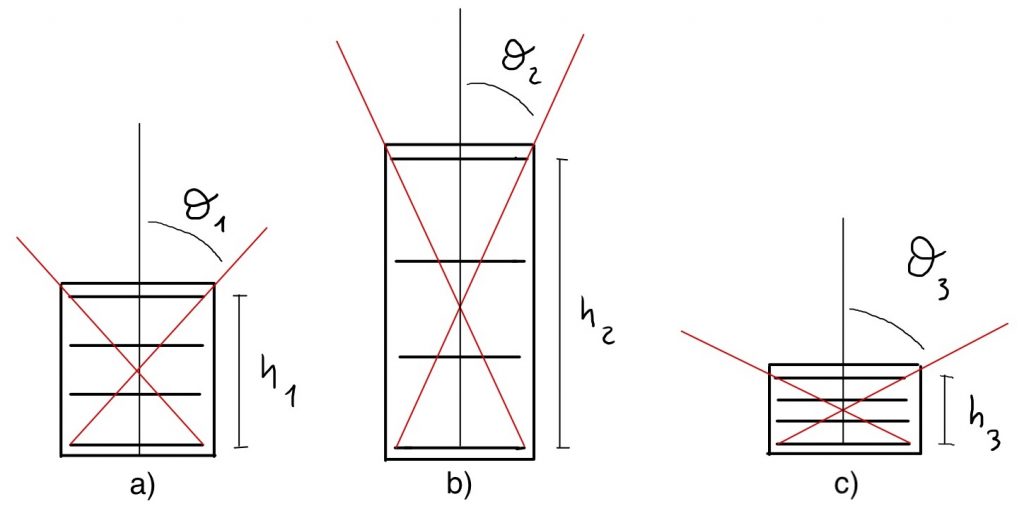
Fig. 3: Disposizione dei piani del rivelatore a diverse altezze come mostrato nelle 3 configurazioni: (a), (b) e (c).

Spesso in rivelatori a più piani si utilizza come “evento da contare” il segnale registrato contemporaneamente da un numero di piani ridotto. Per esempio, con riferimento alla Fig.3(a), si può decidere di contare un evento quando solo tre dei piani di rivelazione registrano un segnale. Prova a disegnare gli angoli theta corrispondenti alle varie “configurazioni di coincidenza”.

Esempi di sorgenti di errori sistematici

Un evento viene registrato se il segnale misurato da tutti i piani di rivelazione avviene entro una finestra temporale. Quando il rivelatore è orientato verso lo zenit solo muoni provenienti dall’alto possono attraversare il rivelatore perché la terra agisce da filtro. Quando il sistema di rivelazione viene ruotato sempre più muoni “orizzontali” possono attraversare il rivelatore in entrambe le direzioni, tuttavia l’angolo di apertura del rivelatore risente dell’effetto di filtro della terra.

La misura di θ che viene fornita è quella dell’angolo tra lo zenit e l’asse dello strumento. E se il rivelatore non fosse perfettamente perpendicolare al terreno? Come potresti verificarlo dai dati?

Ti aspettiamo!

Vuoi imparare a raccogliere i dati prodotti da un rivelatore di muoni, analizzarli e discutere con colleghi e scienziati da tutto il mondo in tempo “reale”? Cerca la sede INFN dove si farà il prossimo ICD più vicina alla tua scuola (https://web.infn.it/OCRA/international-cosmic-day/) e contatta il referente dell’attività. Ti aspettiamo!

Bibliografia

(1) C. Patrignani et al. (Particle Data Group), Chinese Physics C, 40, 100001 (2016): Review of Particle Physics -29. Cosmic Rays.

Misura dei muoni in funzione dell’altezza in atmosfera

da | Mag 14, 2020 | Laboratorio

Il percorso didattico che presentiamo ripercorre l’esperienza di un progetto realizzato nell’ambito dei Percorsi per le Competenze Trasversali e per l’Orientamento (PCTO), ex Alternanza Scuola-Lavoro. Il progetto, denominato MoCRiS (Measurement of Cosmic Ray in Stratosphere), nasce da una collaborazione tra l’ABProject, OCRA INFN Roma1 (Istituto Nazionale di Fisica Nucleare Outreach Cosmic Ray Activities) ed il Liceo Scientifico di Cariati. Questa collaborativa ha consentito l’interazione tra il mondo della scuola, quello della ricerca e quello della tecnologia ed ha fornito, a tutti i partecipanti, la possibilità di apprendere da un ampio spettro di esperienze e professionalità. Gli alunni, sono stati coinvolti dalla progettazione alla realizzazione della sonda, nello studio dei principi teorici della fisica e delle tecnologie aerospaziali, nonché nella fase del lancio del pallone aerostatico che ha raggiunto la quota di 34111 metri. Scopo principale del lancio la misura del flusso di raggi cosmici in funzione della quota eseguito tramite due rivelatori di particelle di tipo ArduSiPM sviluppati dall’INFN Sezione di Roma.

Fig. 1: Foto del team MoCRiS.

Strumentazione utilizzata

L’esperimento MoCRiS è composto da un pallone aerostatico e di una navicella con forma ottagonale contenente diversi strumenti in parte replicati per garantire una tolleranza ai guasti. Per l’analisi che proponiamo utilizzeremo i dati raccolti dai seguenti strumenti di bordo:

  • Sistema di navigazione satellitare GPS
  • Sensore di temperatura
  • Sensore di pressione
  • Due rivelatori particelle ArduSiPM
  • Due camere GoPRO (video+foto)
  • Cattura polveri

 

Calcolo della spinta di Archimede

Il pallone MoCRiS è stato riempito con circa 8 metri cubi di elio (???=0.1784 kg/m3) e librato in aria (????=1.225 kg/m3). Il principio di Archimede afferma che:

“ogni corpo immerso in un fluido riceve una spinta verticale dal basso verso l’alto, uguale, per intensità, al peso del fluido spostato”.

  • Quale è la forza che spinge il pallone in alto alla partenza ?
  • Quale è la forza che spinge il pallone alla partenza ?

Svolgi l’esercizio e poi confronta la tua soluzione con il video:

1-Spinta Archimede

 

Dati da elaborare

Per prima cosa scarica i dati del computer di bordo e dei sistema di acquisizione dei rivelatori ArduSiPM: ComputerDiBordo, DatiRivelatoriArduSiPM.

Poi, dopo aver visionato i video tutorial, ti proponiamo di analizzare tu stesso i dati dell’esperimento con l’obiettivo di riprodurre i grafici mostrati di seguito.

Misura della temperatura in funzione dell’altezza

 

Se hai visionato i video tutorial, prova a riprodurre il grafico in Fig.2

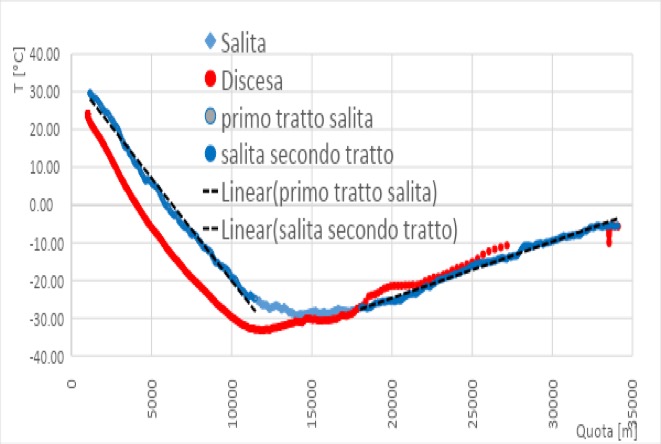Fig.2: Andamento della temperatura esterna in funzione della quota nella fase di salita e discesa della sonda. I due fit mostrano le diverse dipendenze lineari rispettivamente nella troposfera e nella stratosfera

Esercizio: realizziamo un nuovo grafico con 2 serie dati differenti!

I dati raccolti dal sensore di temperatura esterna hanno evidenziato una diminuzione della temperatura fino ad un minimo di -29.30 °C alla quota di 15.291 metri (ore 9:58 UTC), nella fase di salita e di -33.20 °C alla quota di 11.777 metri, nella fase di discesa (ore 10:55 UTC). I dati della temperatura esterna in funzione della quota sono sintetizzati nel grafico di figura 2. Dal grafico si nota che i due andamenti della curva, prima e dopo il minimo, sono pressoché lineari ma con pendenze diverse. La risalita della temperatura all’aumentare della quota, dopo il punto di minimo, avviene più lentamente rispetto alla diminuzione della temperatura all’aumentare della quota prima del minimo.

L’interpretazione di questi dati deve tener conto di alcune nozioni di termodinamica dell’atmosfera sintetizzate nella Fig.3. La dipendenza della temperatura dalla quota è lineare a tratti e presenta delle inversioni di pendenza delle rette che ne descrivono l’andamento da uno strato dell’atmosfera ad un altro. Questo dipende da come la radiazione solare interagisce con l’atmosfera attraverso i fenomeni di assorbimento e conversione in calore dell’energia solare. Nella Troposfera, infatti, prevale il riscaldamento dal basso perché la luce visibile attraversa l’atmosfera senza quasi essere assorbita ed arriva al suolo e agli oceani riscaldandoli. Essi, poi, riemettono l’energia assorbita sotto forma di radiazione infrarossa, rispetto alla quale l’atmosfera risulta invece opaca e quindi si riscalda. In Troposfera (fino a circa 10.000 metri), quindi, la dipendenza della temperatura dalla quota ha un andamento lineare a pendenza negativa (aumenta la quota e diminuisce la temperatura). In Stratosfera (15.000-50.000 metri), invece, l’effetto prevalente non è dato dal riscaldamento dal basso ma dal riscaldamento che l’atmosfera subisce a causa dell’assorbimento degli UV da parte dell’ozono che, a tali quote, è molto abbondante. In questo caso la dipendenza della temperatura dalla quota ha un andamento lineare a pendenza positiva (la temperatura aumenta con la quota) [Approfondimento].

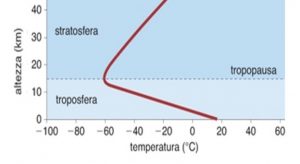Fig.3: Variazione della temperatura e della densità dell’atmosfera in funzione della quota. Ref. http://www.treccani.it/enciclopedia/chimica-atmosferica_%28Enciclopedia-Italiana%29/

Un’altra informazione importante che si può dedurre dalle pendenze dei due tratti (Troposfera e Stratosfera) della curva di figura 2, ad esempio nella fase di salita della sonda, è il gradiente termico cioè la variazione di temperatura ad esempio ogni 1000 metri di quota. Nel tratto di Troposfera e Stratosfera i dati mostrano un gradiente termico rispettivamente di -5.5 °C e 1.5 °C ogni 1000 metri di quota (coefficienti angolare delle rette con cui è stato fatto il fit dei due tratti in figura 2) in accordo con i valori in letteratura [Approfondimento 1 e 2].

Misura della pressione  in funzione dell’altezza

 

Se hai visionato i video tutorial, prova a riprodurre i grafici in Fig.4 e 5.

 

Nel plot di Fig.4 è riportato l’andamento della pressione in funzione della quota rilevata dal sistema GPS per la fase di salita e discesa della sonda. Le due curve, come ci si aspetta, sono esattamente sovrapponibili a dimostrazione del buon funzionamento dei sensori in perfetto accordo con la curva teorica espressa dall’equazione (1) che, come è noto, esprime la dipendenza della pressione atmosferica (P misurata in kPa) dalla quota (h espressa in metri) [Algoritmo di conversione]: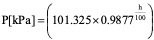

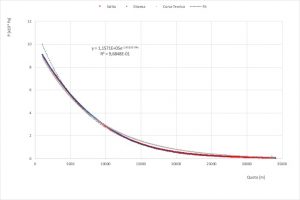Fig.4: Andamento della pressione in funzione della quota

La Fig.5 mostra l’andamento della temperatura in relazione alla variazione della pressione durante la fase di salita e quella di discesa della sonda.  La curva di discesa non coincide esattamente con quella di salita per via del fatto che tra le due fasi è trascorso del tempo (la salita è durata 84 minuti e la discesa 24 minuti) durante il quale le condizioni meteo sono leggermente cambiate. Le curve mostrano, nei tratti non vicini al minimo, la dipendenza lineare tra temperatura e pressione in modo inversamente e direttamente proporzionale rispettivamente prima e dopo il minimo. Questo comportamento si capisce meglio se ricordiamo che all’aumentare della quota la pressione diminuisce (vedi Fig.4) e la temperatura in funzione della quota ha il comportamento spiegato nella Fig.2.

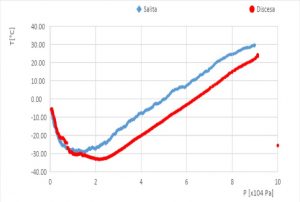Fig.5: Andamento della temperatura esterna in funzione della pressione.

La rivelazione dei raggi cosmici

La nostra atmosfera è bombardata continuamente dai raggi cosmici. Quest’ultimi sono costituiti da particelle di  alta energia, prevalentemente protoni, che colpiscono l’alta atmosfera generando a cascata una pioggia di particelle che raggiunge la superficie terrestre. All’inizio del secolo scorso l’enigma di una misteriosa radiazione penetrante fece arrovellare i fisici dell’epoca, nel 1911 il fisico Domenico Pacini utilizzando dei rivelatori immersi in acqua intuì l’origine extraterrestre di questa radiazione, nel 1912 Victor Hess con delle misure con palloni aerostatici fino alla quota di 5300 metri fornì una delle prove principi della natura extraterrestre.Il nome di raggi cosmici fu coniato nel 1925 dal fisico americano Robert Millikan che sosteneva erroneamente una natura elettromagnetica e non particellare. Nel 1930 i fisici Regener-Pfotzer con una serie di lanci di palloni stratosferici misurarono il flusso di particelle trovando che tale flusso aumentava fino alla quota di circa 20 000 metri per poi diminuire (Fig. 6).[Approfondimenti]

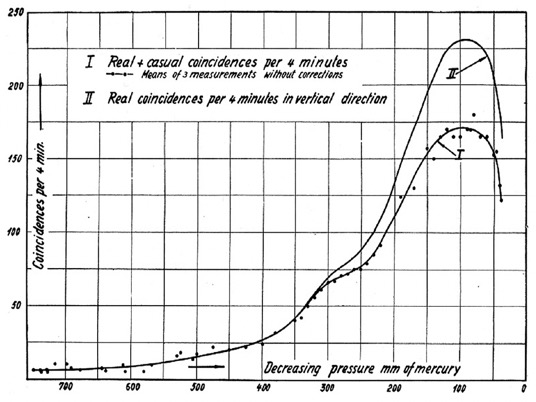Fig.6: Misura originale di Regener-Pfotzer con il flusso in funzione della pressione atmosferica.

Quello che si misura in atmosfera non sono in realtà i raggi cosmici primari, ma lo sciame di altre particelle che viene generato dalla particella primaria nel suo impatto con le molecole dell’atmosfera, queste a sua volta generano, interagendo con la materia, altre particelle. Quindi per ogni particella primaria si genera uno sciame, o una doccia (shower in inglese) di particelle che ricopre a terra un’area di qualche chilometro quadro (che dipende dall’energia della particella primaria che ha generato lo sciame). [Approfondimenti]

Le particelle secondarie, che arrivano a terra sono per la maggior parte muoni il loro flusso, a livello del mare, è di circa una per cm2 al minuto. Le particelle del primario possono avere energie anche superiori ai 1019 eV ben dieci milioni di volte più energetiche di quelle del più grande acceleratore costruito dall’uomo (LHC al CERN di Ginevra), le particelle di energia molto elevata sono anche molto rare (qualcuna per Km2 all’anno) mentre la maggior parte dei cosmici primari possiede energie dell’ordine di decine di GeV. [Approfondimenti]

Per misurare il flusso di particelle generate dagli sciami in atmosfera nel progetto MoCriS si utilizzano due rivelatori di particelle ArduSiPM il cui principio di rivelazione è basato su scintillatori, caratteristica di questi rivelatori è la loro leggerezza (circa 200 g) ed il loro basso consumo (< 2.5 watt), che li hanno resi ideali per un lancio con pallone di tipo light, quale quello di MoCriS.  Mettendo in relazione il numero di conteggi alle misure di pressione si ottiene il grafico in Fig.7. Notare la corrispondenza della misura con la prima effettuata nel 1930, e il massimo di Regener-Pfotzer a circa 10000 Pascal corrispondenti a circa 100 g/cm2, che ci indica la quantità di materiale attraversata dallo sciame. La misura del massimo di Regener-Pfotzer ad intervalli più o meno regolari può essere messa in relazione all’attività solare, quindi alla diminuzione del campo magnetico del Sole che ci scherma in parte dalla radiazione cosmica [Approfondimento].  MoCriS come il precedente progetto EOS ha dimostrato la fattibilità di queste misure con i rivelatori ArduSiPM utilizzando palloni aerostatici tipo light.

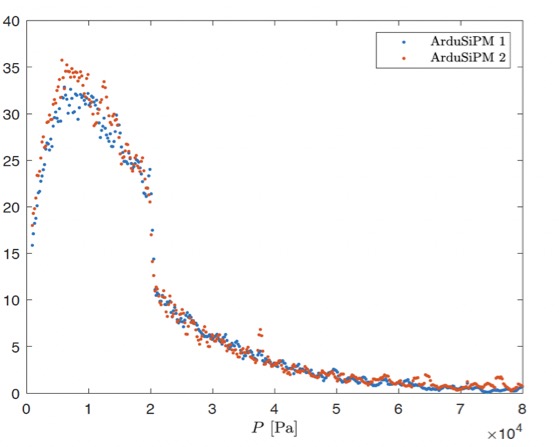Fig.7: Andamento del flusso di raggi cosmici in funzione della pressione. Dati MoCRiS

Per concludere:

9-Import dati ArduSiPM (Video)

Se hai visionato i video tutorial, prova a riprodurre il grafico in Fig.7

 

Bibliografia e sitografia

https://sites.google.com/view/particle-detectors/ardusipm-literature/mocris-balloon-thesis

Misura dei muoni in funzione della profondità in acqua

da | Mag 14, 2020 | Laboratorio

Esperimento Pacini

Nei primi anni del ’900 gli scienziati scoprirono l’esistenza di radioattività naturale sulla Terra, e si chiesero da dove questa radioattività avesse origine; tra le varie ipotesi la più accreditata era che fosse dovuta a radiazioni provenienti dalla crosta terrestre. La soluzione dell’enigma richiese

una decina di anni, e fu una delle imprese intellettuali più emozionanti della storia della scienza. Essa portò alla scoperta che buona parte della radiazione trae origine da sorgenti extraterrestri – e alla radiazione extraterrestre fu in seguito dato il nome di “raggi cosmici”.

Sappiamo oggi che i raggi cosmici sono particelle (in maggioranza protoni) che urtano l’atmosfera terrestre apparentemente da ogni direzione, a velocità prossime a quelle della luce. Le loro energie sono tra le più alte osservate in natura (anche cento milioni di volte l’energia delle particelle dell’acceleratore LHC al CERN di Ginevra): devono quindi provenire da potentissimi acceleratori cosmici, probabilmente in resti di supernova e nei dintorni di buchi neri supermassicci. Il meccanismo di accelerazione fu spiegato da Enrico Fermi nel 1949 (raggi cosmici di minore energia provengono, invece, dal Sole.) Arrivare a questa conclusione fu difficile: la contemporanea esistenza di radiazione cosmica e di radiazione terrestre rendeva delicati gli esperimenti. [[Approfondimenti]

Durante una serie di esperimenti condotti tra il 1907 e il 1911, il fisico italiano Domenico Pacini condusse importanti studi sulla radiazione naturale. Nel suo esperimento conclusivo, condotto nel giugno 1911 presso l’Accademia Navale di Livorno e confermato nel lago di Bracciano un paio di mesi più tardi, Pacini, grazie a una tecnica sperimentale innovativa, osservò che le radiazioni penetranti naturali diminuivano nel passaggio dalla superficie dell’acqua a pochi metri sott’acqua (sia in mare sia nel lago), dimostrando così per primo che una parte rilevante di tali radiazioni non poteva venire dalla Terra.

Il numero di raggi cosmici che arrivano sulla Terra dipende molto dalla loro energia E, e cala velocemente con essa. La distribuzione in energia (il cosiddetto spettro) dei raggi cosmici (Fig.1) è abbastanza ben descritta localmente da una legge di potenza (ossia da una funzione del tipo E−p), con p (il cosiddetto indice spettrale) numero positivo. Dopo la regione di basse energie, dominata da raggi cosmici provenienti dal Sole (parte del cosiddetto vento solare), tale spettro diventa più ripido con p ∼ 2.7 per valori dell’energia inferiori a ∼ 1000 TeV. Per valori superiori dell’energia si ha un ulteriore aumento di pendenza, con p ∼ 3; il punto in cui tale cambio di pendenza ha luogo viene denominato “ginocchio”. Per energie ancora più alte (oltre un milione di TeV) lo spettro dei raggi cosmici torna ad essere meno ripido, dando luogo a un ulteriore cambio di pendenza che viene chiamato “caviglia”.

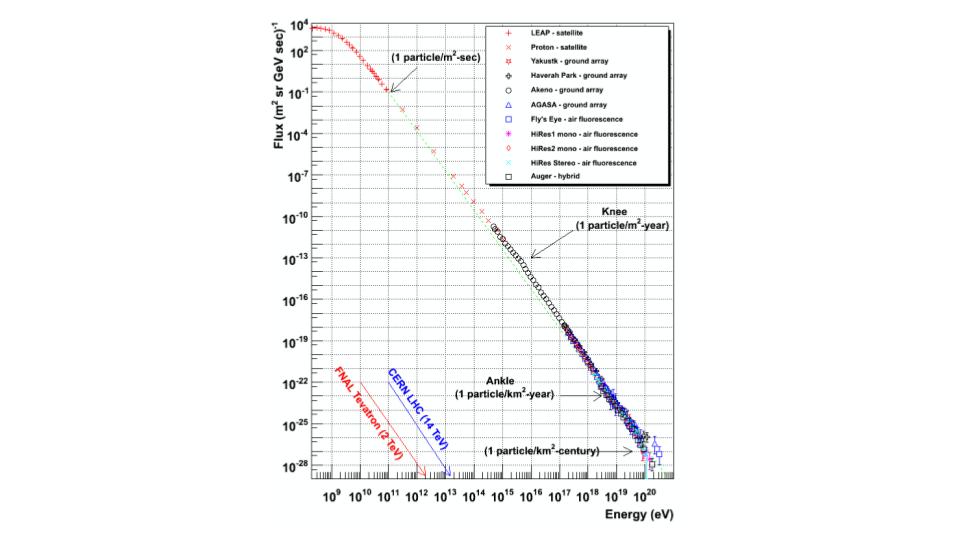Fig.1: Spettro in energia dei raggi cosmici.

La maggioranza delle particelle di alta energia in arrivo di raggi cosmici sono protoni, circa il 10% sono nuclei di elio (particelle alfa), e l’1% sono neutroni o nuclei di elementi più pesanti. Questi insieme costituiscono il 99% dei raggi cosmici, e gli elettroni e i fotoni costituiscono il grosso del restante 1%.

I raggi cosmici che incidono sull’atmosfera (detti raggi cosmici primari) producono in generale particelle secondarie che possono arrivare alla superficie della Terra, attraverso il meccanismo dei cosiddetti “sciami” moltiplicativi, che comporta il susseguirsi di una complessa storia di interazioni a catena, produzioni, assorbimenti e decadimenti spontanei. Senza l’effetto schermante dell’atmosfera terrestre, raggi cosmici che rappresentano un grave pericolo per la salute ci colpirebbero direttamente (persone che vivono in alta montagna o che fanno frequenti viaggi in aereo sono soggette a una dose supplementare misurabile di radiazioni).

Pacini e le misure di attenuazione in acqua

L’opinione che la radioattività naturale provenisse esclusivamente dalla disintegrazione di materiali radioattivi nella crosta terrestre fu messa in dubbio dal fisico italiano Domenico Pacini. A conclusione di una serie di misure del tasso di ionizzazione in montagna, sulla superficie di un lago, e sul mare Tirreno, nel 1911 Pacini realizzò un innovativo esperimento immergendo un elettroscopio a una distanza di circa 300 metri dalla costa di Livorno di fronte all’Accademia Navale e poi nel lago di Bracciano, misurando una significativa diminuzione della radioattività in profondità rispetto alla superficie, e dimostrando quindi che parte della radiazione veniva dall’alto.

Riprodurre l’esperimento di Pacini con un elettroscopio è molto difficile; le condizioni di misura sottomarina pongono grandi problemi sperimentali, fortunatamente oggi disponiamo di strumenti migliori. In un periodo successivo agli esperimenti di Pacini fu introdotta, per la misura del passaggio di particelle cariche, la tecnica basata sul tubo contatore di Geiger. Esso è costituito da un tubo contenente un gas a bassa pressione; lungo l’asse del tubo è teso un filo metallico, isolato dal tubo stesso. Tra il filo e il tubo si stabilisce un’alta differenza di potenziale, dell’ordine di 1000 volt. Quando una particella carica attraversa il tubo e colpisce una delle molecole del gas, la ionizza, creando, tramite il processo della moltiplicazione a valanga, coppie di cariche positive e negative. L’impulso elettrico risultante è testimone dell’avvenuto contatto con una radiazione ionizzante – il contatore Geiger ha quindi grande sensibilità alle particelle cariche.

La misura in lago

Nella misura originale in invaso, abbiamo usato un contatore Geiger. Lo strumento è equipaggiato con un tubo contatore di alta precisione che consente di rilevare raggi alfa, beta e gamma. I dati vengono memorizzati in una memoria interna, e possono essere letti con interfaccia USB.

Fig.2: Gli studenti mentre effettuano le misure nel lago di Calcione.

Per immergere lo strumento in acqua, esso è stato inserito in una scatola di plastica impermeabile opportunamente zavorrata con una massa di 2 kg legata tramite un filo di 0.5 m di lunghezza, dopo che su di essa avevamo effettuato opportuni test atti a verificare l’effettiva impermeabilizzazione fino a 13 metri di profondità.

Le misure sono state effettuate immergendo da una piattaforma galleggiante (usata per prelevare l’acqua da immettere nell’acquedotto locale) fissa al centro del lago su un fondale di 13 metri il contatore inserito nella scatola impermeabile descritta sopra, impostato per salvare in memoria i dati una volta al minuto. Tale apparato sperimentale è stato tenuto immerso a 1 metro di profondità per 17 minuti, a 3 metri per 18 minuti, e a 5 metri per 13 minuti. Infine è stata misurata la radiazione in superficie per 26 minuti.

Le distribuzioni delle misure sono risultate a vista gaussiane: per questo motivo si è ritenuto ragionevole scartare le misure che si discostano per più di 3 deviazioni standard dalla media (tre in totale) ritenendo probabile che fossero affette da un errore intrinseco. Come risultato della misura è stato considerato il valore medio per ciascuna profondità dopo questa operazione, e come errore stimato l’errore quadratico medio diviso N − 1, dove N è il numero di misure rimaste dopo la rimozione degli eventi nelle code della distribuzione.

La radiazione penetrante di origine extraterrestre che giunge al suolo è costituita prevalentemente da adroni (soprattutto protoni e pioni provenienti dagli sciami generati dall’interazione dei protoni con l’atmosfera) e soprattutto da muoni; mentre la lunghezza d’onda d’interazione inelastica ad alta energia degli adroni in acqua è di λH = 83 cm, la lunghezza di attenuazione dei muoni è di un ordine di grandezza più grande, e dunque contribuisce meno all’effetto di profondità.

Possiamo stimare pari a f ∼ 0.25 la frazione di radioattività sulla superficie del mare proveniente da particelle (per quanto detto prevalentemente adroni) di origine direttamente o indirettamente cosmica con lunghezze di attenuazione confrontabili con il metro. Il nostro modello per la misura di radioattività R in funzione della profondità d è dunque:

 

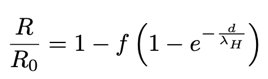
(1)

 

dove R0 è la radioattività misurata in superficie. Come già detto, ai tempi di Pacini l’interazione degli adroni di alta energia con la materia non era conosciuta; in ogni caso si riteneva che le particelle che costituivano la radiazione fossero raggi gamma. La lunghezza di attenuazione gamma usata da Pacini per i suoi calcoli era di 33 cm. In ogni caso, la lunghezza di attenuazione è tale da garantire che 3 metri di acqua schermino quasi totalmente la radiazione dall’alto.

Una verifica sperimentale quantitativa di un modello a due parametri (la frazione di radiazioni “cosmiche” e la lunghezza di attenuazione) non ha evidentemente molto senso visto che abbiamo a disposizione solo tre punti sperimentali; possiamo tuttavia assumere l’equazione (1) come modello asintotico, in accordo con quanto fatto da Pacini. Nella Fig.3 le misure di R/R0 vengono confrontate con l’equazione, e l’accordo è qualitativamente soddisfacente.

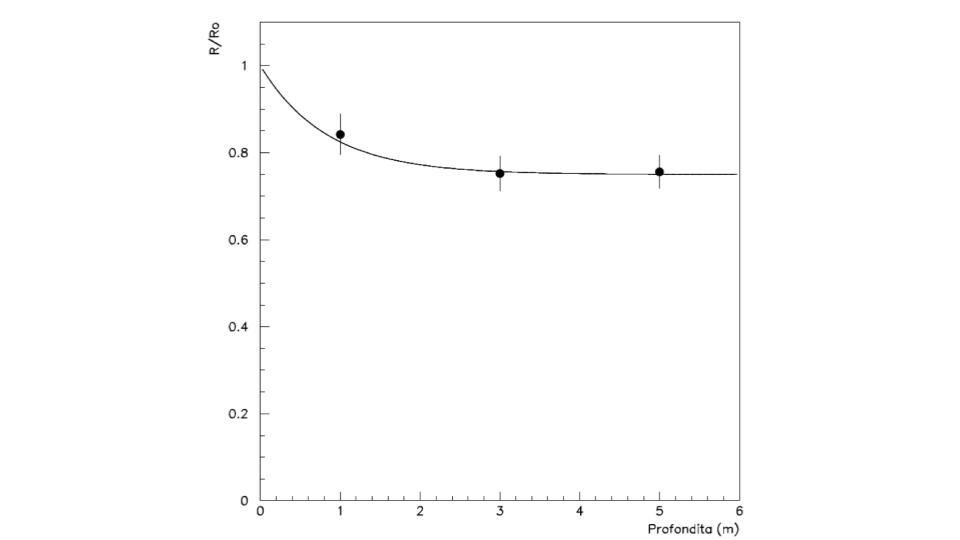Fig.3: I risultati della misura in lago

La misura in mare

Alcuni studenti del liceo scientifico Cecioni di Livorno hanno partecipato alla misura che è stata effettuata, dopo vari rinvii per maltempo, il giorno 11/12/2019 al largo del porticciolo di S. Jacopo presso l’Accademia Navale di Livorno (Fig.4 e Fig.5).

Fig.4: Vista dell’Accademia Militare durante le misure del dicembre 2019.

Fig.5: Gli studenti del liceo Cecioni e il corpo accademico dell’Accademia Navale (a sinistra il Prof. Morganti, a destra il il T.V. Coi e il C.F: Capecchi)

Il setup utilizzato era ridondante e consisteva in due contatori “Gamma Scout” posti in scatole impermeabili “Peli case” (Fig.6). A differenza delle misure in invaso, l’esperienza in mare aperto è soggetta ad effetti esterni che possono influire sulla misura, ad es. presenza di vento e forti correnti marine.

Fig.6: Setup sperimentale usato per le misure presso l’Accademia Navale.

Gli studenti hanno effettuato le misure e verificato la diminuzione di eventi in funzione della profondità (Fig.7). Durante le misure, una delle scatole ha avuto un problema di tenuta e l’acqua ha temporaneamente bloccato il funzionamento di un contatore. La presenza di vento e corrente opposti ha modificato l’assetto in mare, le misure a profondità maggiore di 3 m (punti chiari) sono stati corretti per l’effetto dell’angolo rispetto alla verticale (punti scuri). Dal fit dei punti sperimentali si trova una frazione di radiazione alla superficie di circa 0.26 ed una lunghezza di attenuazione pari a circa 28 cm, le bande del 68% sono calcolate sul parametro f soltanto (Fig.8).

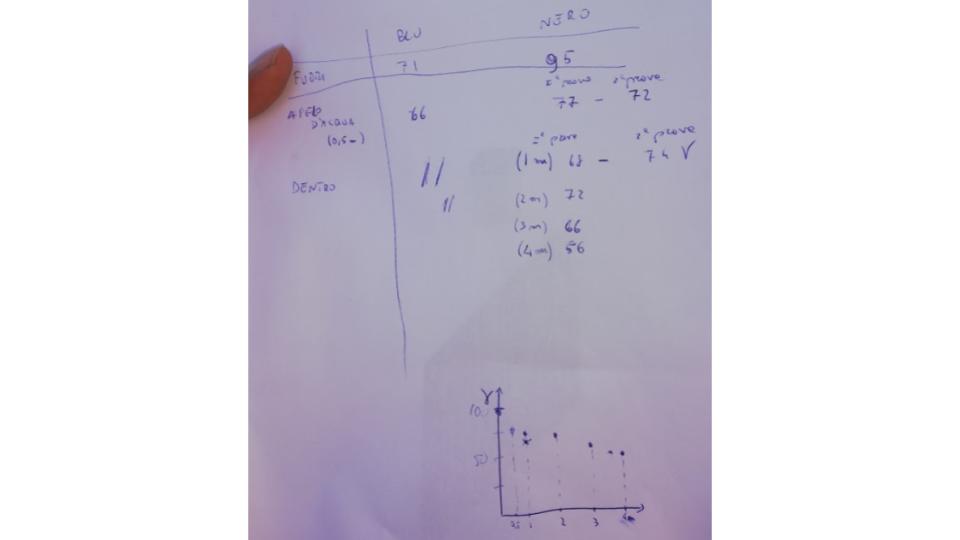Fig.7: Logbook “online” tenuto dagli studenti.

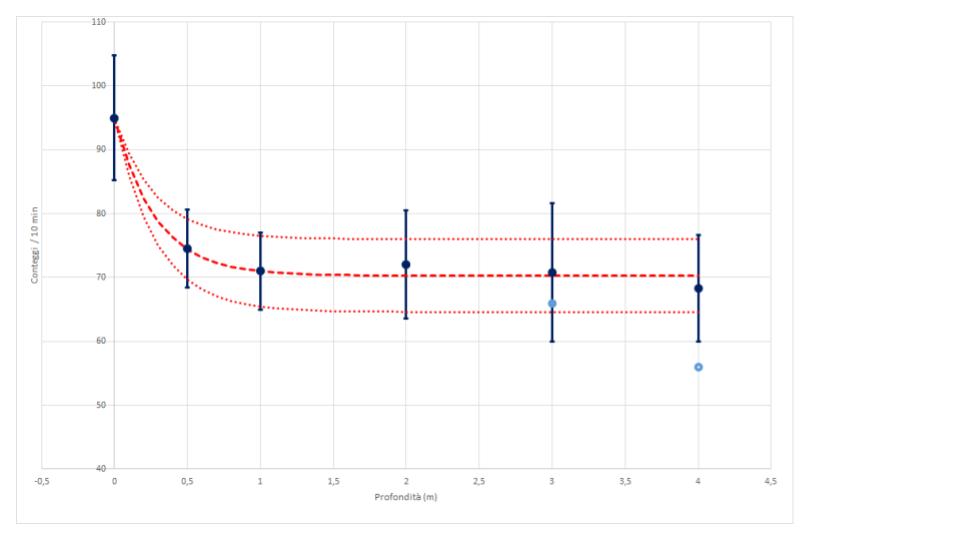Fig.8: Misura dell’attenuazione ottenuta in mare.

Vuoi provare ad analizzare anche tu i dati raccolti dagli studenti del Liceo Cecioni?

  • Scarica il file Excel
  • Prova a riprodurre il grafico della Fig.8

 

Conclusioni

La misura dell’effetto di schermatura delle radiazioni con il metodo di Pacini è un’esperienza entusiasmante per gli studenti. Da una parte, a differenza di quanto avviene in laboratorio, sono impegnati in una serie di misure “en plein air” con la difficoltà di risolvere problematiche sul momento ed individuare anche i motivi per un comportamento anomalo dei dati dovuto a motivazioni di sistematica. D’altra parte, i dati sono descritti da una funzione esponenziale a due parametri che permette l’analisi statistica raffinata e, quindi, un’introduzione a concetti basilari di trattamento statistico dei dati come il fit con il metodo dei minimi quadrati che può essere svolto a mano dallo studente. Utilizzando un foglio elettronico e le funzioni di base, è possibile determinare i valori ottimali dei parametri e uno studio delle bande di errore.