Le misure che descriviamo in questa sezione e che rendiamo disponibili per l’analisi dati sono state eseguite durante l’INTERNATIONAL COSMIC DAY (ICD). L’ICD è un progetto internazionale per gli Istituti Superiori organizzato dall’Istituto Nazionale di Fisica Nucleare (https://web.infn.it/OCRA/international-cosmic-day/) in collaborazione con DESY Accelerator Laboratory (Amburgo) e con altri Laboratori di Fisica e Istituti in tutto il mondo. Durante la giornata dedicata ai raggi cosmici gli studenti entrano in contatto con l’attività di ricerca in fisica, portano a termine un piccolo esperimento sui raggi cosmici, analizzano i dati, confrontano i propri risultati con gli altri gruppi collegati da altre università o centri di ricerca nel mondo, lavorano per un giorno come in una collaborazione internazionale e pubblicano i risultati.

Cosa dobbiamo misurare?

I raggi cosmici primari (come spiegato qui) non riescono a raggiungere la superficie terrestre perché interagiscono (si scontrano) con gli atomi dell’atmosfera creando una cascata di particelle secondarie. Questi sciami di particelle secondarie durano pochi miliardesimi di secondo e, una volta arrivati a terra, possono coprire un’area di diversi chilometri quadrati. Tra le particelle cariche che arrivano a terra, i muoni sono quelli più facilmente misurabili. Nonostante risultino invisibili all’occhio umano, il metodo usato dai ricercatori, per evidenziarne il passaggio, consiste nel farli interagire con la materia sensibile (particolari materiali che diano un segnale elettrico o luminoso una volta che vengono attraversati da queste particelle). La registrazione di questi fenomeni fornisce ai ricercatori informazioni sul passaggio delle particelle e dell’energia che hanno rilasciato. Questa strumentazione prende il nome di rivelatore (“detector” in inglese). Il rivelatore utilizzato in questa esperienza è il CosmicRayCube (CRC), per una descrizione dettagliata del rivelatore usato per queste misure vi rimandiamo al link: CRC. In sintesi il rivelatore è fatto da 4 piani di rivelazione messi in coincidenza.

Muoni

Ricapitoliamo velocemente quali sono le caratteristiche delle particelle che andremo ad osservare, i muoni:

• sono simili agli elettroni, ma hanno una massa 200 volte maggiore;
• attraversano materiali poco densi (come le pareti degli edifici e i nostri corpi) perdendo poca energia;
• ogni minuto veniamo attraversati da centinaia di muoni, essi contribuiscono alla dose di radioattività naturale a cui siamo soggetti;
• nonostante abbiano una vita media di 2.2 milionesimi di secondo, arrivano fino alla superficie della terra e si fermano dopo aver attraversato decine di metri sottoterra in strati di roccia.

Misura del flusso di raggi cosmici in funzione dell’angolo di zenit

Il flusso di muoni a terra non è uniformemente distribuito. Analizzando le direzioni di arrivo di queste particelle in funzione dell’angolo che esse formano con lo zenit locale, si scopre che il flusso massimo si ha per θ=0° ossia per particelle che arrivano perpendicolarmente alla superficie terrestre. Il flusso diminuisce continuamente all’aumentare dell’angolo tra la direzione di incidenza e lo zenit. A 90° il flusso è minimo. Come è spiegato in Review of Particle Data (1), la distribuzione dei valori misurati può essere descritta usando una funzione cos².

Diversi effetti sono responsabili di questo comportamento, tra questi, il cammino percorso dalle particelle cosmiche attraverso l’atmosfera.

I muoni, prodotti a 15 km di altezza nell’atmosfera, sono il prodotto di decadimenti di altre particelle come pioni e kaoni prodotti nell’interazione tra i raggi cosmici primari e gli atomi nell’atmosfera. Come si vede dal link, facendo uso della sola interpretazione fisica classica, queste particelle non potrebbero arrivare a terra (visto che la loro vita è di solo 2,2 μs), ma l’interpretazione fornita da Einstein con la relatività speciale ci spiega come fanno i muoni, che si muovono a velocità prossime a quelle della luce, a percorrere tutta l’atmosfera fino ad arrivare alla superficie terrestre. Quindi ci aspettiamo di vedere solo i muoni che riescono a percorrere lo strato di atmosfera prima del loro decadimento.

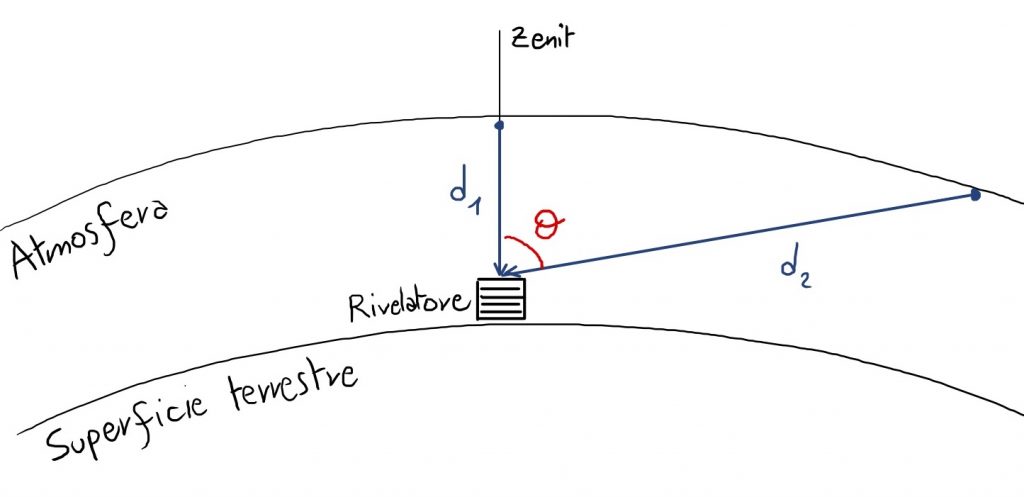
Fig.1: Rappresentazione dei cammini (d1 e d2) effettuati da due muoni prodotti in atmosfera e diretti verso il rivelatore posto sulla superficie terrestre.

Con riferimento alla Fig.1,  i muoni che arrivano perpendicolarmente alla superficie terrestre (arrivano lungo la direzione dello zenit locale), percorrono meno strada in atmosfera, mentre, per angoli di incidenza elevati, angolo theta rispetto allo zenit, la distanza viene estesa. Con un angolo di incidenza di 90°, la distanza che il muone deve percorrere attraverso l’atmosfera fino alla superficie della terra è di circa 400 km (anziché 15 km). Solo pochi alti picchi di energia riescono a coprire questo percorso. In conclusione, maggiore è l’angolo dallo zenit, maggiore è la distanza percorsa, maggiore sarà la probabilità che i muoni decadano prima di raggiungere la superficie terrestre e quindi il flusso sarà minore.

LA TECNICA SPERIMENTALE

Il numero di muoni (conteggi, C) incidenti nel rivelatore in un intervallo di tempo (T) prende il nome di rate (R=C/T) espresso in particelle al secondo. La presa dati risulta quindi sintetizzata in questo modo:

• Prendo dati per un tempo T
• Conto il numero di particelle registrate C
• Calcolo il rate R delle particelle come: R = C / T (part/sec)

Esempio:

Prendo dati per 100 secondi (T=100 secondi)

Lo strumento registra C=1000 particelle

R= C / T = 1000/100 = 10 particelle/secondo

Fissato un tempo, misurare la dipendenza dei conteggi dall’angolo di inclinazione (Fig.2).

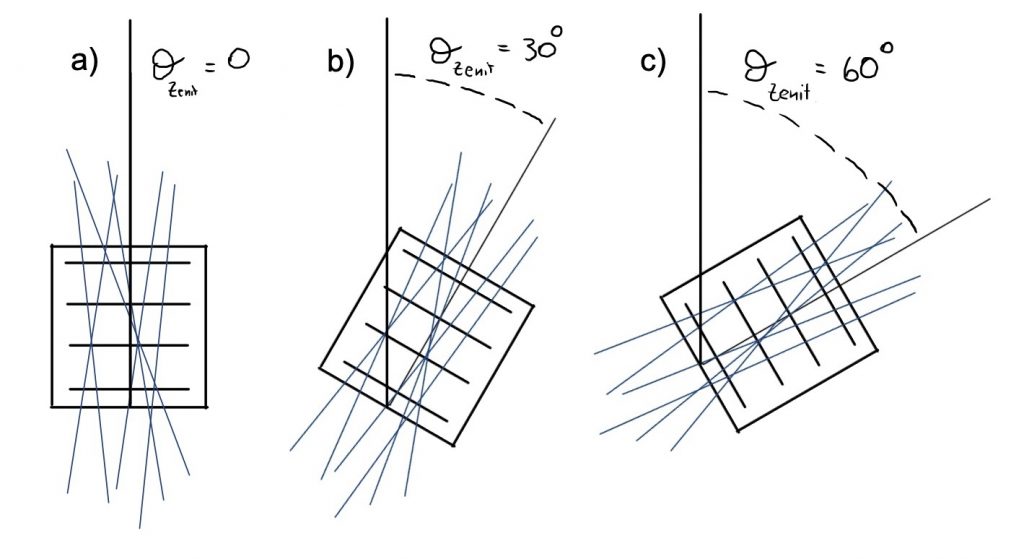
Fig. 2: Rappresentazione della configurazione sperimentale, il rivelatore, inizialmente posizionato con l’asse parallelo allo zenit locale (a), viene inclinato ad angoli via via sempre maggiori: 30° (b), 60° (c) fino a posizionarlo orizzontalmente.

Raccolta dati

Per questa parte dell’esperienza è conveniente utilizzare un foglio di calcolo, puoi usare quello che preferisci o che usi già, per esempio Excel, Calc o un foglio di lavoro google.

Noi li abbiamo inseriti in un foglio di lavoro google che trovi in: shorturl.at/kvEO0

Quando sono presenti più misure dello stesso angolo, come puoi stimare la misura? La migliore stima del valore vero è la media aritmetica dei valori ottenuti nelle varie misure. Tieni conto che alcune misure di C potrebbero riferirsi a tempi di acquisizione diversi (l’intervallo di conteggio è indicato tra parentesi nella legenda).

Riempi una tabella con i dati (θ, C)!

Ogni misura sperimentale di una grandezza è affetta da errori sistematici e statistici. Per quanto riguarda la stima dell’errore delle singole misure ci concentreremo sull’aspetto statistico. Possibili spunti per individuare le sorgenti di errori sistematici sono forniti al termine dell’esperienza. Noi misuriamo il numero di raggi cosmici che provengono dallo spazio nello stesso intervallo di tempo. Se ripetiamo la misura diverse volte, non otteniamo sempre lo stesso risultato ma possiamo fare delle considerazioni di carattere statistico cioè possiamo dire qual è la probabilità di avere un certo risultato. La distribuzione di probabilità che descrive, con buona approssimazione, i fenomeni di conteggio di raggi cosmici è la distribuzione di POISSON. La distribuzione di probabilità di Poisson si applica quando si ha a che fare con eventi rari riferiti ad uno specifico intervallo di tempo. L’errore statistico associato a questo tipo di distribuzione è √C, dove C è il numero di eventi per ogni misura. Siccome stiamo analizzando il rate delle particelle, l’errore relativo a questa quantità deriva dalla propagazione degli errori dividendo, quindi, l’errore del numero di conteggi (√C) per il tempo T. Se volessimo avere errori relativi confrontabili per ogni misura cosa avremmo potuto fare durante la presa dati? (Partecipate all’ICD per conoscere la risposta!)

ANALISI DEI DATI

1. Calcolare il rate dei muoni: R = C / T (part/sec) per ciascun angolo e associare il relativo errore statistico
2. Disegnare il grafico: rate (asse y) in funzione dell’inclinazione theta (asse x)
3. Ci aspettiamo una dipendenza da cos²θ. Come si confronta questa previsione coi tuoi dati?
4. Può essere pratico calcolare grandezze come cos²θ. Prova a rifare il grafico in funzione di cos²θ e verifica che i dati sono approssimabili ad una retta. Calcola il coefficiente angolare della retta usando la regressione lineare.
5. Come riportato nell’articolo Review of Particle Data (1), l’andamento del cos²θ è riferito all’intensità (I = R/(G*ε) ) dei raggi cosmici e non al rate. Ricordiamo che G è il fattore geometrico di accettanza (espressa in m²sr) ed ε rappresenta le efficienze del rivelatore (si veda il link ); entrambi G e ε sono proprietà intrinseche della strumentazione utilizzata. Sapresti spiegare cosa sarebbe cambiato se avessimo utilizzato l’intensità dei muoni anziché il rate?
6. Cosa succederebbe se disegnassi il rapporto di R(θ)/R₀ e I(θ)/I₀ (sull’asse y) in funzione dell’angolo θ (asse x)? R₀ e I₀ sono rispettivamente il rate e l’intensità dei muoni che arrivano verticali (θ=0).

Riflettiamo sulla “geometria del rivelatore”

Con riferimento alla Fig.3, come pensi possa variare il rate/intensità delle particelle osservate modificando la distanza tra i piani del rivelatore dalla configurazione (a) alla configurazione (b)? Cosa succede invece se si passa da (a) a (c)?

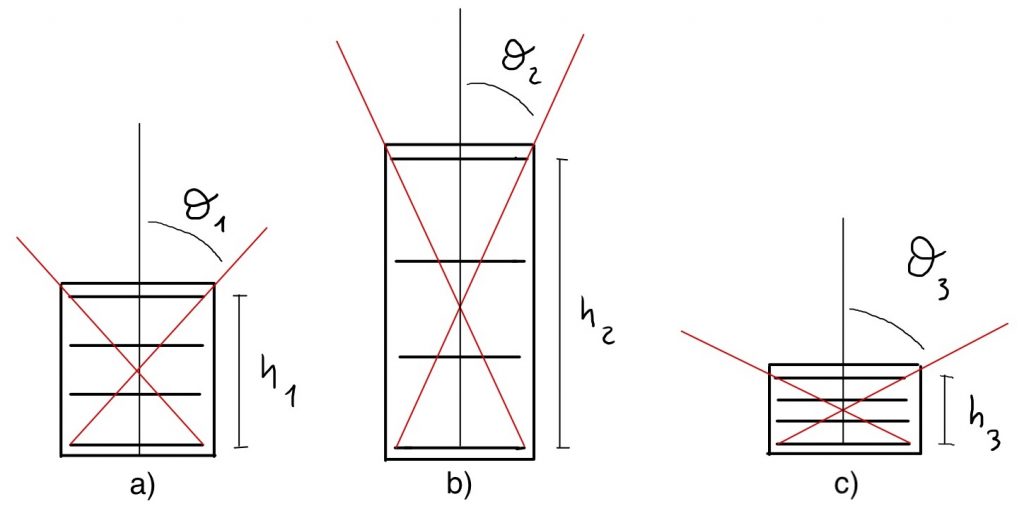
Fig. 3: Disposizione dei piani del rivelatore a diverse altezze come mostrato nelle 3 configurazioni: (a), (b) e (c).

Spesso in rivelatori a più piani si utilizza come “evento da contare” il segnale registrato contemporaneamente da un numero di piani ridotto. Per esempio, con riferimento alla Fig.3(a), si può decidere di contare un evento quando solo tre dei piani di rivelazione registrano un segnale. Prova a disegnare gli angoli theta corrispondenti alle varie “configurazioni di coincidenza”.

Esempi di sorgenti di errori sistematici

Un evento viene registrato se il segnale misurato da tutti i piani di rivelazione avviene entro una finestra temporale. Quando il rivelatore è orientato verso lo zenit solo muoni provenienti dall’alto possono attraversare il rivelatore perché la terra agisce da filtro. Quando il sistema di rivelazione viene ruotato sempre più muoni “orizzontali” possono attraversare il rivelatore in entrambe le direzioni, tuttavia l’angolo di apertura del rivelatore risente dell’effetto di filtro della terra.

La misura di θ che viene fornita è quella dell’angolo tra lo zenit e l’asse dello strumento. E se il rivelatore non fosse perfettamente perpendicolare al terreno? Come potresti verificarlo dai dati?

Ti aspettiamo!

Vuoi imparare a raccogliere i dati prodotti da un rivelatore di muoni, analizzarli e discutere con colleghi e scienziati da tutto il mondo in tempo “reale”? Cerca la sede INFN dove si farà il prossimo ICD più vicina alla tua scuola (https://web.infn.it/OCRA/international-cosmic-day/) e contatta il referente dell’attività. Ti aspettiamo!

Bibliografia

(1) C. Patrignani et al. (Particle Data Group), Chinese Physics C, 40, 100001 (2016): Review of Particle Physics -29. Cosmic Rays.