Il telescopio per muoni cosmici della metropolitana di Toledo a Napoli

Il percorso ci porterà alla scoperta del rivelatore istallato nel 2014 nella stazione di Toledo (Fig.1), la più bella stazione metropolitana d’Europa! Guarda il Video

Nel percorso “Raggi Cosmici” Abbiamo imparato molto sul muone e come si può rivelare. In questo percorso vedremo come un telescopio installato sotto 40 m di roccia può rivelare queste particelle che hanno una massa 200 volte quella dell’elettrone e che vivono solo 2.2 us. Il telescopio descritto in questo percorso è simile al Cosmic Ray Cube (CRC), solo che è costituito da 10 piani rispetto ai 4 del CRC.

Fig.1: Il telescopio installato nella stazione Toledo della metropolitana di Napoli, a destra è visibile anche il Totem multimediale che permette, tra l’altro, di registrare i dati e di renderli accessibili in rete.

I 10 piani del telescopio sono realizzati da bacchette di materiale scintillante plastico che emette un debole impulso di luce quando è attraversato da particelle cariche come i muoni. Le barre sono disposte ortogonalmente tra loro sul piano orizzontale (direzione x e y) ed hanno ciascuna dimensioni di 4 x 1 x 40 cm³. Ogni barra è otticamente accoppiata con una fibra ottica ad un fotomoltiplicatore a silicio (Silicon Photomultiplier – SiPM) che assorbe la luce emessa dallo scintillatore e la trasforma in una corrente elettrica che, attraverso una scheda di elettronica, permette l’accensione dei 200 LED per la ricostruzione in 3D dei muoni che attraversano il rivelatore. Quando un muone attraversa il telescopio, viene quindi visualizzata una traccia luminosa come nella Fig.1. Inoltre, il telescopio è accoppiato ad un Totem touchscreen multimediale che permette l’acquisizione dei dati del telescopio tramite una connessione seriale, la ricostruzione della direzione di provenienza dei muoni e la visualizzazione della loro traccia sullo schermo (Fig.2).

Fig.2: Ricostruzione della traccia di un muone rivelato dal telescopio come visualizzata  sul Totem.

Richiedendo che almeno su sei piani del telescopio ci sia un LED acceso, si ottiene una rate di 4 eventi al minuto.

Ascolta la descrizione del telescopio dalla voce di chi lo ha progettato e costruito, insieme ai colleghi dei Laboratori Nazionali del Gran Sasso e della Sezione INFN di Napoli. http://people.na.infn.it/~totem/Video/Attanasio.htm

Decodifica Tracce

I dati acquisiti dal telescopio possono essere scaricati dal sito http://people.na.infn.it/~totem.

I file “Muoni_Eventi_anno_mese_giorno.txt” contengono i dati “raw”, mentre i file “Muoni_Orario_anno_mese_giorno.txt” contengono i dati ricostruiti per ciascuna faccia del telescopio. Le quattro colonne di questi ultimi file rappresentano: numero identificativo dell’evento, data di acquisizione e angolo che la traccia forma con la verticale rispettivamente nella faccia XZ e YZ (theta_x e theta_y).

Un evento “raw” è rappresentato nel seguente modo (Fig.3):

STF337

00000100200F00C018030020040180

008018010018018018010030010010

ST indica che c’è un nuovo evento, mentre F337 il numero di evento espresso in esadecimale. Le due righe successive sono due stringhe esadecimale che, come per il CRC, ci permettono di ricostruire quali bacchette di scintillatore sono state colpite dal passaggio del muone e, quindi, quali LED si sono accesi sulle due facce del telescopio. La prima stringa rappresenta la vista XZ, vista MASTER, mentre la seconda la vista YZ, vista SLAVE. Ogni stringa ha 30 caratteri, ogni 3 caratteri indicano un piano. Trasformandoli in binario otteniamo 12 canali dei quali i primi due non vanno considerati. In particolare, per il telescopio di Toledo i primi 3 caratteri esadecimali danno l’informazione dei canali accesi (“1”), relativi al piano più basso e così via. Si tenga presente che una stringa di tutti 0, in alcuni casi, può indicare che quel piano, sebbene sia stato interessato dal passaggio della particella, non ha “acceso” alcuna bacchetta di scintillatore e questo in genere accade per sola inefficienza di quello scintillatore o del sistema scintillatore-WLS-SiPM.

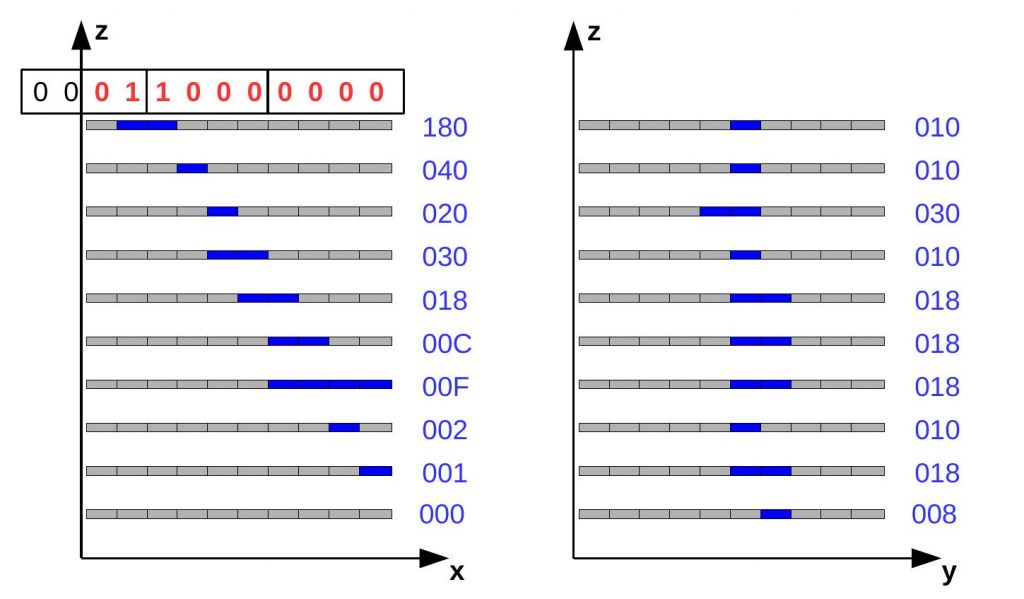
Fig.3: Decodifica dei dati Raw per ricostruire la traccia dei muoni.

Come ricostruire le due rette che indicano il passaggio del muone sulle due facce a partire dai dati raw e la retta nello spazio identificata dagli angoli theta e phi è spiegato nel percorso Misura della rate di muoni cosmici.

In questo percorso ti proponiamo i seguenti:

? Esercizi interattivi

Partiremo dai dati contenuti nei file “Muoni_Orario_anno_mese_giorno.txt”, che, come abbiamo detto, contengono gli angoli che la traccia forma con la verticale rispettivamente nella faccia XZ e YZ. Questi identificano la direzione nel piano del muone che attraversa il telescopio, in quanto la loro tangente rappresenta il coefficiente angolare della retta/traccia. Scritte le rette nei due piani, possiamo ricavare theta e phi che descrivono la retta nello spazio.

Ogni esercizio viene svolto tramite un foglio di lavoro (notebook) messo a disposizione da Google Colab e utilizzando il linguaggio di programmazione Python.

I dettagli dell’analisi sono indicati passo passo nel Google Colab.

Quando si analizza un numero elevato di dati discreti, al fine di dare un senso all’analisi dei dati stessi, si rende necessaria la suddivisione in intervalli di valori che comprendono tutti i dati che vi appartengono. Si suddividono gli eventi dell’arrivo dei muoni in base all’inclinazione che hanno rispetto una determinata direzione, si creano così degli intervalli in cui andiamo a contare tutti gli eventi che hanno un angolo compreso tra i due estremi dell’intervallo.

Quando abbiamo un insieme di dati ed andiamo a contare quante volte essi si presentano all’interno di ogni intervallo che abbiamo definito, parliamo di distribuzione di frequenze cioè una funzione che può essere rappresentata elencando tutte le coppie ordinate in una tabella avente come colonne l’intervallo di valori considerato e la frequenza assoluta (il numero di casi che si contano nell’intervallo). Il modo più semplice per elaborare un insieme di dati statistici e di trarre le prime osservazioni sull’andamento del fenomeno che si sta osservando è quello di rappresentarli graficamente. Generalmente il modello di rappresentazione più utilizzata per i fenomeni fisici osservati è quello dell’istogramma che è un particolare diagramma cartesiano che ha sulle ascisse valori discreti x_i o intervalli di valori (che chiamiamo bin), sulle ordinate l’altezza della colonna rappresentante il numero delle frequenze in funzione dei valori presi in considerazione.

Introduciamo dunque due termini tecnici che spesso saranno utilizzati nelle attività di questo percorso che sono “bin” (o binning) e “fit” (o fitting). Per costruire un istogramma bisogna innanzitutto considerare il numero totale di dati, bisogna scegliere il binning ovvero la divisione del dominio della variabile sulle ascisse, cioè si deve definire il numero di intervalli e la loro ampiezza, infine si devono conteggiare i dati da associare ai singoli bin (cioè contare il numero di dati che cade in ogni singolo intervallo).

Dopo aver trasformato i dati sperimentali raccolti in un istogramma si cerca di ricavare una curva che sia in grado di “raccontare” meglio il comportamento dei dati. Un metodo tipico è quello del “best fit” ossia la ricerca di una curva che abbia come caratteristica essenziale che la curva approssimante si avvicini il più possibile ai punti.

Per scegliere la curva di fitting si deve valutare quale funzione matematica potrebbe essere più rappresentativa per l’analisi del fenomeno. Possiamo immaginare una regressione di tipo lineare o polinomiale o esponenziale o sinusoidale … o la “distribuzione normale” (o gaussiana). Il nome “normale” deriva dalla convinzione che molti fenomeni fisici e biologici si distribuiscono con frequenze più elevate nei valori centrali e con frequenze progressivamente minori verso gli estremi della variabile. Questa distribuzione è caratteristica dei fenomeni casuali. L’equazione della funzione normale è la seguente:

Si tratta di una curva dalla classica forma a campana che ha un massimo nel valore medio dei valori misurati e può essere più o meno stretta a seconda della dispersione dei valori attorno alla media; la dispersione si misura con la deviazione standard.

? Esercizio 1: 

Puoi scaricare i dati del telescopio, convertirli in una tabella e infine, dopo un po’ di elaborazione, costruire degli istogrammi relativi alle distribuzioni delle direzioni di arrivo dei muoni. Potrai modificare interattivamente il numero dei bin di ciascun istogramma e verificarne l’effetto nella visualizzazione dei dati. Diversi aspetti fisici andrebbero considerati per spiegare la forma delle distribuzioni ottenute, se sei curioso contattaci e approfondiremo insieme questi aspetti.

Vai all’esercizio: https://colab.research.google.com/drive/1mhNjQ6xpcp7L23RL9PABGIyFpEurAzvE?usp=sharing

? Esercizio 2:  Puoi trovare quale tra le curve proposte meglio si adatta alle distribuzioni trovate tramite la procedura di fit. Potrai scegliere tra due diverse funzioni polinomiali, la gaussiana o la gaussiana asimmetrica. Di ciascuna potrai variare i parametri iniziali e scoprire come variano dopo il fit.

Vai all’esercizio: https://colab.research.google.com/drive/1gRwq45HP0QCPKbbRaS_QiDhaduUu4H5r?usp=sharing