In laboratorio con noi

Per poter studiare i raggi cosmici è necessario prima di tutto osservarli.

In questa sezione verranno descritte alcune tecniche di rivelazione usate negli esperimenti a terra.

Poi, per chi si vorrà cimentarsi, nella sezione laboratori sarà possibile fare l’analisi dei dati di esperimenti veri e propri, alcuni dedicati alla didattica e alla divulgazione come il telescopio-Totem multimediale situato nella stazione Toledo della metropolitana di Napoli, altri dedicati alla ricerca come l’osservatorio Auger nella pampa Argentina, che con i suoi 1600 rivelatori sparsi su un territorio di 3000 km², è il più grande esperimento mai realizzato per lo studio di raggi cosmici ad altissima energia.

La tecnica delle coincidenze

I conteggi di un singolo rivelatore sono dovuti, oltre che ai raggi cosmici, a radioattività ambientale, a rumore dell’elettronica e in generale a eventi casuali non correlati tra loro. Inoltre, quando i raggi cosmici colpiscono un singolo rivelatore, non è possibile individuare il tipo di particella. Il metodo utilizzato, sia per ridurre gli eventi casuali sia per discriminare le particelle cariche, è la tecnica delle coincidenze.

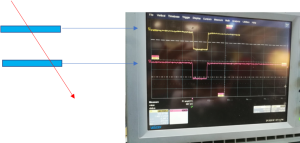
Una coincidenza è il segnale emesso contemporaneamente da più rivelatori collegati tra loro. Poiché il segnale ha sempre larghezza finita, la coincidenza si ha se i segnali si sovrappongono entro un certo intervallo temporale Se abbiamo più contatori sovrapposti e questi emettono un segnale in coincidenza è probabile che, al livello del mare, si tratti di un muone perché più penetrante rispetto ad altre particelle cariche che non riuscirebbero ad attraversare tutti i contatori. Naturalmente più sono i piani più alta è la probabilità di rivelare un muone da un segnale di coincidenza.

Ma le coincidenze non sono tutte vere, infatti se 2 rivelatori sono posti uno sull’altro si possono avere i seguenti casi:

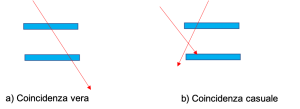
a) una particella li attraversa entrambi;

b) due particelle attraversano contemporaneamente ciascuna un rivelatore.

In entrambi i casi si parla di coincidenza ma nel primo si ha una coincidenza vera mentre nel secondo una coincidenza casuale. Per effettuare misure precise, soprattutto se gli eventi sono molto rari, è necessario stimare le coincidenze casuali per poterle eliminare. La rate delle coincidenze casuali è legata al numero dei rivelatori dalla legge:

$R_{n}=nR^{n}_{singola}\cdot \tau ^{n-1}\$

Dove n è il numero dei rivelatori e $\tau$ è il tempo durante il quale si ha la coincidenza. All’aumentare del numero dei contatori le coincidenze casuali diminuiscono drasticamente. Facciamo un esempio: consideriamo dei rivelatori di area 1 m² che contano 300 particelle al secondo (R_singola = 300 Hz) e mettiamoli in coincidenza con un intervallo temporale di 400 ns (t = 400×10^-7 s). Il numero di coincidenze casuali sarà:

con 2 contatori R₂ = 7,2×10^-2 Hz
con 3 contatori R₃ = 1,28×10^-7 Hz

Aggiungendo un solo contatore in coincidenza la rate di coincidenze casuali diminuisce di 5 ordini di grandezza. La tecnica delle coincidenze viene utilizzata anche per rivelare gli sciami. In questo caso si utilizzano rivelatori posti uno accanto all’altro e se si registra una coincidenza allora vuol dire che fanno parte dello stesso sciame. Bruno Rossi realizzò il primo circuito di coincidenza tra più di 2 rivelatori e perfezionò la tecnica che permetteva di metterli in coincidenza anche a grande distanza.

Il telescopio per muoni

Il dispositivo più semplice per rivelare raggi cosmici è costituito da 2 contatori messi uno sopra l’altro in configurazione telescopica, cioè con i centri allineati su una linea retta chiamata asse, e connessi ad un circuito di coincidenza. Questo permette di:

selezionare una particolare direzione di provenienza all’interno dell’angolo solido individuato dall’accettanza geometrica (più i piani sono distanti più l’angolo solido è piccolo, più precisa è la direzione ma minore il campo visivo);
selezionare il tipo di particella in funzione del numero di piani di contatori (più sono i piani, più le particelle che li attraversano in coincidenza sono penetranti).

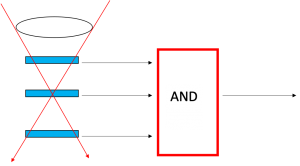
Un rivelatore di questo tipo è quello che normalmente viene chiamato telescopio per raggi cosmici e utilizzato per rivelare muoni.

Se i piani di rivelatori, oltre a contare le particelle, sono in grado di anche individuare il loro punto di impatto è possibile ricostruirne la direzione di arrivo. Naturalmente all’aumentare del numero dei piani aumenta la precisione con la quale viene ricostruita la retta che individua la traiettoria.

Infatti le coincidenze tra i rivelatori possono anche essere casuali (2 muoni che arrivano anche da direzioni diverse ma contemporaneamente sui rivelatori), in tal caso se i piani sono solo 2 sicuramente tra i 2 punti passerà una retta, ma se i piani sono 3 i punti d’impatto non è detto che siano allineati e quindi la coincidenza verrà scartata. Possono anche aversi 2 punti soltanto nei primi 2 rivelatori e nessun segnale sul terzo. Anche in questo caso la coincidenza viene scartata perché la particella non è penetrante quindi non è un muone. Quindi ogni evento che non interessi i 3 rivelatori con un allineamento dei punti lungo una retta, entro la risoluzione spaziale dei rivelatori, non sarà considerato. Anche se i contatori non sono traccianti aumentare il numero dei piani permette di ridurre drasticamente il numero delle coincidenze casuali come è stato spiegato nella sezione tecnica delle coincidenze.

Ricordiamo che il primo esempio di telescopio di raggi cosmici venne messo a punto da Bruno Rossi nel 1931 nel suo laboratorio di Arcetri. Nella figura è mostrato il primo esemplare con due rivelatori costituiti da tubi Geiger-Muller. Come si può vedere il dispositivo può essere orientato per misurare le particelle che giungono da diverse direzioni.

Rate e flusso

Lo scopo di tutti gli esperimenti di raggi cosmici è determinare il flusso di particelle di una data specie in uno specifico intervallo di energia, cioè misurare il numero di particelle per unità di area, di tempo, di angolo solido e con un’energia nell’intervallo $\Delta E$ , quindi il numero di particelle per m^-2, s^-1, sr^-1, eV^-1. Questo è il cosiddetto flusso differenziale di particelle con una certa energia in un determinato angolo solido. Per farlo bisogna identificare e contare le particelle che attraversano il rivelatore con un’energia E compresa tra E e E+ $\Delta E$ .

Spesso non è possibile determinare l’energia delle singole particelle ma si misurano tutte le particelle a partire da una certa energia di soglia E₀. Si parla allora di flusso integrale di particelle con energia > E₀, con unità di misura particelle per m^-2, s^-1, sr^-1. Quello che si misura però in ogni esperimento di RC è il rate di conteggi dN/dt e non il flusso! Quindi, in ogni esperimento, i dati sono registrati per un intervallo di tempo T durante il quale N_i particelle del tipo i (che attraversano il rivelatore ed interagiscono con il suo materiale attivo) sono identificate e contate.

Come ottenere il flusso a partire dal rate misurato è il punto cruciale di ogni esperimento.

Il telescopio presentato nella precedente sezione è un rivelatore ideale di raggi cosmici fatto da 2 strati di rivelatore di area A posti a distanza z. Una particella che arriva entro l’angolo solido $\Delta\Omega$ produrrà un segnale su ognuno di essi. Il conteggio di coincidenze C nel telescopio dipende dalle dimensioni dei rivelatori e dalla loro posizione relativa, cioè dalla geometria dei sensori, ma anche dall’intensità della radiazione nello spazio circostante e dall’efficienza di rivelazione $\epsilon$ .

Lo scopo dei ricercatori è calcolare il flusso della radiazione a partire dal rate di coincidenze misurato e dalle caratteristiche del telescopio.

Per un telescopio ideale il fattore di proporzionalità tra il rate di coincidenze C e l’intensità della radiazione $\Phi$ e’ il potere di raccolta $\Gamma$ del telescopio. Cioe’ si ha $C=\Gamma \Phi$ . Se l’intensità è isotropa, cioè $\Phi=\Phi_0$ , il fattore di proporzionalità è il cosiddetto fattore geometrico G, noto anche come accettanza geometrica, cioè si ha $C=G \Phi_0$ . L’accettanza è in pratica la capacità di raccolta del rivelatore. Il punto critico è quindi la determinazione dell’accettanza geometrica G. Nel caso semplice di un telescopio composto da un singolo piano di rivelazione su cui incide un flusso isotropo di particelle si calcola che l’accettanza non è la semplice area ma A $\pi$ perché il rivelatore ‘raccoglie’ particelle con direzione di incidenza fra 0 e $\pi/2$ . Questo in sostanza perché l’area di rivelazione vista dalle particelle incidenti dipende dalla loro direzione di arrivo (descritta dall’angolo zenitale $\theta$ ed azimutale $\phi$ ) in una piccola regione angolare $d\Omega = sin\theta d\phi d\theta$ . L’accettanza è quindi misurata in m² sr.

Ecco allora che in generale il flusso di particelle di data energia E è dato da: $\Phi(E) = \frac{Ci}{\Delta E \Delta T G \epsilon}$ cioè dal rapporto tra il numero di coincidenze misurate per la particella i divisa per la sua energia, il tempo di misura $\Delta T$ , l’accettanza del telescopio G e la sua efficienza $\epsilon$ nel selezionare e rivelare la particella i. L’efficienza quindi indica il numero di particelle contate rispetto a quelle effettivamente passate attraverso il rivelatore.

Apparati di sciami

Lo studio dei raggi cosmici attraverso la rivelazione degli sciami atmosferici estesi è molto difficile. Si pensi che al livello del mare, uno sciame di altissima energia (10¹⁹ eV) ha dissipato circa il 90% della sua energia in aria! Quindi le numerosissime particelle (anche milioni) che giungono al suolo trasportano una piccolissima frazione dell’energia del raggio cosmico primario.

L’osservazione degli sciami atmosferici viene effettuata con i cosiddetti “apparati di sciame”. Essi sono costruiti distribuendo un certo numero di rivelatori su aree enormi (generalmente dell’ordine di 10⁴ – 10⁶ m²), a costituire una struttura a scacchiera (griglia o “array”) più o meno regolare. Con questi apparati si cerca di compilare la carta di identità del raggio cosmico primario, cioè determinare la sua energia, la sua natura (cioè il tipo di nucleo) e la direzione di arrivo. Le prime due sono informazioni molto difficili da ricostruire perché, non osservando al suolo direttamente il primario, esse sono disperse tra le numerosissime particelle che compongono uno sciame esteso e devono essere determinate spesso applicando sofisticate tecniche di analisi. I rivelatori servono a misurare le differenti componenti che costituiscono uno sciame: elettromagnetica, muonica e adronica. Essi sono tipicamente scintillatori plastici, bidoni di acqua, resistive plate chamber (RPC), calorimetri o rivelatori di neutroni, ma, come ricordato, possono essere utilizzati anche telescopi Cherenkov o fluorescenza e antenne radio. I rivelatori possono essere posizionati in superficie o sotto alcuni metri di terra per meglio rivelare la componente penetrante costituita dai muoni. Le caratteristiche di un apparato di sciame sono definite dall’area coperta dai rivelatori (area instrumentata), dalla distanza tra essi e dal rapporto tra la superficie sensibile di tutti i rivelatori e l’area instrumentata (il cosiddetto “coverage”). Sono queste quantità che stabiliscono l’energia minima che può essere rivelata (l’energia di soglia) ed in generale l’intervallo di energia che può essere indagato. Se si vuole un dispositivo con una soglia di energia molto bassa, i rivelatori devono essere molto ravvicinati, fino al caso limite di copertura totale (coverage >90%, come nel caso dell’esperimento ARGO-YBJ). Gli sciami di bassa energia sono infatti piccoli, cioè hanno poche particelle distribuite su aree contenute, quindi per rivelarli è necessario coprire con rivelatori tutta l’area instrumentata per non perdere alcuna particella. Viceversa, se si è interessati alla rivelazione di sciami prodotti da raggi cosmici di alta energia, poiché in questo caso gli sciami contengono milioni di particelle distribuite su aree ampie anche km², allora i rivelatori possono essere meno numerosi e posti a maggiore distanza tra loro (in questi casi il coverage è dell’ordine del percento). Fino ad arrivare al caso limite di un esperimento come l’osservatorio Pierre Auger che, per indagare le energie più alte mai osservate, impiega rivelatori distanti 1.5 km tra loro e distribuiti su un’area di circa 3000 km² .

Gli apparati di sciame misurano essenzialmente due quantità, il numero di particelle e la direzione di arrivo dello sciame e con esse si compila la carta di identità della particella primaria. Visto che uno sciame esteso è composto da diversi tipi di particelle, quello che viene misurato è il numero totale di particelle cariche, principalmente elettroni e positroni (questa è la cosiddetta ‘size’ dello sciame). Negli apparati più sofisticati si possono misurare separatamente i diversi tipi di particelle, elettroni, muoni e adroni, con specifici rivelatori. La determinazione della size è importante perché da essa si risale all’energia della particella primaria che ha dato origine allo sciame. La direzione di arrivo dello sciame è invece determinata con la cosiddetta ‘tecnica del tempo di volo‘. Le particelle quando colpiscono i rivelatori non lo fanno contemporaneamente, soprattutto negli sciami inclinati. Misurando il ritardo temporale tra la prima particella che arriva su un qualsiasi rivelatore e le altre è possibile determinare l’angolo di incidenza dello sciame e quindi della particella primaria.

Ricordiamo come nel 1956 il gruppo di Bruno Rossi fu il primo a mettere in funzione negli USA un apparato di sciame in grado di determinare contemporaneamente la size e la direzione di arrivo (esperimento Agassiz). Fu questa una vera rivoluzione nello studio dei raggi cosmici di altissima energia. Con esso infatti si rivelarono per la prima volta eventi con più di 109 particelle, quindi con energie maggiori di 10¹⁸ eV!

L’esperimento ARGO-YBJ.

L’Italia ha una lunga tradizione nello studio dei raggi cosmici con apparati di sciame. L’INFN ha ideato, progettato e realizzato l’esperimento EAS-TOP, in funzione fino al 2000 presso i LNGS, e l’esperimento ARGO-YBJ situato a 4300 m slm in Tibet ed in funzione fino al 2013. Partecipa da 20 anni all’osservatorio Pierre Auger in Argentina per lo studio delle particelle di più alte energie mai osservate.

L’osservatorio Pierre Auger. Ref. www.auger.org

Laboratori

Esperimenti didattici

Gli esperimenti descritti di seguito sono realizzati con semplici dispositivi con i quali è possibile rivelare i muoni cosmici e descriverne il loro comportamento. In ogni esperimento è dedicato alla descrizione di una misura sperimentale e con i dati messi a vostra disposizione sarete guidati nell’analisi che porterà alla misura di una grandezza fisica dei muoni:

Esperimenti per la ricerca

Alcuni esperimenti hanno reso pubblici parte dei loro dati che è possibile scaricare direttamente dai siti ufficiali delle collaborazioni. In questa sezione verrete guidati nell’esplorazione di tali dati e nella loro analisi e potrete confrontare i vostri risultati con quelli ufficiali.

L’osservatorio Pierre Auger

Spazio Docenti

Una breve selezione di materiali di supporto per lo sviluppo di un progetto didattico all’interno delle classi

Glossario

Approfondisci i termini che vengono usati in questo percorso e nei laboratori.